题目内容
(12分) 已知在正方体ABCD —A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG =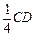 .
.
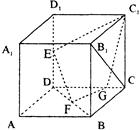
(1)求证:EF⊥B1C;
(2)求EF与G C1所成角的余弦值;
 .
. 
(1)求证:EF⊥B1C;
(2)求EF与G C1所成角的余弦值;
(1)略
(2)
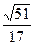
解:如图建立空间直角坐标系O—xyz,
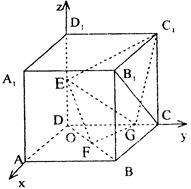
设正方体的棱长为4,则E (0,0,2),F (2,2,0),
C (0,4,0),B (4,4,0),C1(0,4,4),B1(4,4,4),G (0,3,0) . (2分)
(1)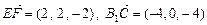 ,
,
∴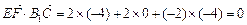 .
.
∴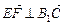 . ∴EF⊥B1C. (5分)
. ∴EF⊥B1C. (5分)
(2)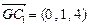 ,
,
∴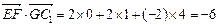 .
.
又∵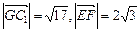 ,
,
∴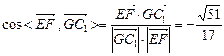 . (10分)
. (10分)
因为,EF与GC1所成角的范围为(0,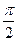 ]
]
所以,EF与GC1所成角的余弦值为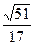 12分
12分

设正方体的棱长为4,则E (0,0,2),F (2,2,0),
C (0,4,0),B (4,4,0),C1(0,4,4),B1(4,4,4),G (0,3,0) . (2分)
(1)
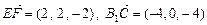 ,
,∴
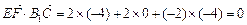 .
.∴
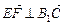 . ∴EF⊥B1C. (5分)
. ∴EF⊥B1C. (5分)(2)
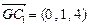 ,
,∴
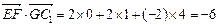 .
.又∵
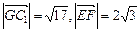 ,
,∴
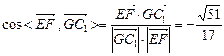 . (10分)
. (10分)因为,EF与GC1所成角的范围为(0,
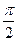 ]
]所以,EF与GC1所成角的余弦值为
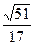 12分
12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
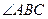 的度数为
的度数为 
 中,
中,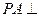 底面
底面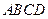 ,
,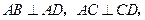
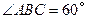 ,
,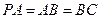 ,
,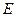 是
是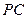 的中点.
的中点.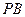 和平面
和平面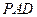 所成的角的大小;
所成的角的大小;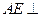 平面
平面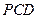 ;
;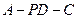 的正弦值
的正弦值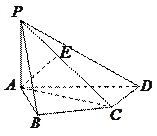
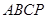 中,
中,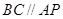 ,
,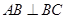 ,
,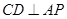 ,
,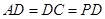 ,
,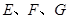 分别是
分别是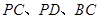 的中点,现将
的中点,现将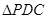 沿
沿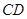 折起,使平面
折起,使平面 平面
平面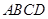 (如图2),且所得到的四棱锥
(如图2),且所得到的四棱锥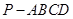 的正视图、侧视图、俯视图的面积总和为8.
的正视图、侧视图、俯视图的面积总和为8.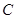 到平面
到平面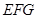 的距离;
的距离;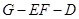 的大小的夹角的余弦值;
的大小的夹角的余弦值;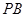 上确定一点
上确定一点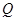 ,使
,使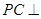 平面
平面 ,并给出证明过程.
,并给出证明过程.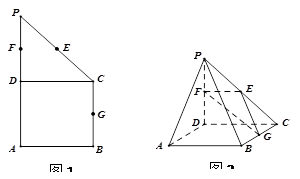
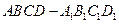 的底面
的底面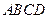 是菱形,
是菱形,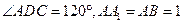 ,点
,点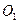 、
、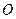 分别是上、下底面菱形的对角线的交点.⑴求证:
分别是上、下底面菱形的对角线的交点.⑴求证: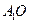 ∥平面
∥平面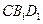 ;⑵求点
;⑵求点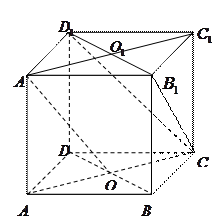
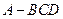 ,
,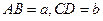 ,
, ,
,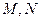 分别为
分别为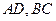 的中点,
的中点,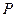 为
为 上一点,则
上一点,则 的最小值是
的最小值是 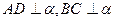 ,AD=4,
,AD=4, ,
,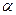 内的轨迹是 ( )
内的轨迹是 ( )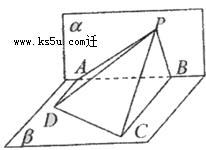
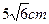 的正四面体内有一点P,它到三个面的距离分别是1cm,2cm,3cm,则它到第四个面的距离为_______________cm .
的正四面体内有一点P,它到三个面的距离分别是1cm,2cm,3cm,则它到第四个面的距离为_______________cm .