题目内容
(本小题12分)
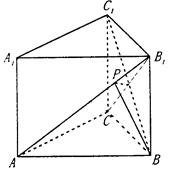
如图,正方体ABCD—A1B1C1D1中,M、N分别为AB、BC的中点.
(Ⅰ)求证:平面B1MN⊥平面BB1D1D;
(II)当点P为棱DD1中点时,求直线MB1与平面A1C1P所成角的正弦值;
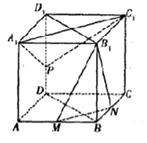
如图,正方体ABCD—A1B1C1D1中,M、N分别为AB、BC的中点.
(Ⅰ)求证:平面B1MN⊥平面BB1D1D;
(II)当点P为棱DD1中点时,求直线MB1与平面A1C1P所成角的正弦值;

(1)略
(2)

(法一)(I)正方体ABCD—A1B1C1D1中, 平面ABCD,
平面ABCD,  平面ABCD,
平面ABCD,  ,连结AC,
,连结AC,  M、N分别为AB、BC
M、N分别为AB、BC
的中点, MN//AC,又四边形ABCD是正方形,
MN//AC,又四边形ABCD是正方形,  ,
,  平面BB1D1D,
平面BB1D1D,
又 平面B1MN,
平面B1MN,
 平面B1MN
平面B1MN 平面BB1D1D (6分)
平面BB1D1D (6分)
(II)设正方体棱长为2,取CD中点H,连C1H、MH,由于MH∥C1B1,MH=C1B1,所以四边形C1HM B1为平行四边形, M B1∥C1H,所以直线C1H与平面A1C1P所成角θ即为直线MB1与平面A1C1P所成角。设H到平面的距离为h,∵P为DD1中点,所以A1P=C1P= ,
, ,
, ,由
,由 得,h=
得,h= ,所以sinθ=
,所以sinθ= ; ( 12分)
; ( 12分)
(法二)
以D为原点,DA、DC、DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,如图所示,则D(0,0,0),A(2,0,0),B(2,2,0),C(0,2,0),D1(0,0,2),A1(2,0,2),B1(2,2,2),C1(0,2,2),P(0,0,x),M(2,1,0),N(1,2,0)
(I)
 ,
, ,
, ,∴
,∴ ,
, ,
,  ,
, ,
, ,
, 平面BB1D1D,又
平面BB1D1D,又 平面B1MN,
平面B1MN,  平面B1MN
平面B1MN 平面BB1D1D (6分)
平面BB1D1D (6分)
(II)设 为平面平面A1C1P的一个法向量,
为平面平面A1C1P的一个法向量, P为DD1中点,P(0,0,1),
P为DD1中点,P(0,0,1), ,
, ,则
,则 ,也就是
,也就是 ,
, ,令
,令 ,
, 又
又 ,设MB1与平面A1C1P所成角为θ,
,设MB1与平面A1C1P所成角为θ,
则

 , ( 12分
, ( 12分
 平面ABCD,
平面ABCD,  平面ABCD,
平面ABCD,  ,连结AC,
,连结AC,  M、N分别为AB、BC
M、N分别为AB、BC的中点,
 MN//AC,又四边形ABCD是正方形,
MN//AC,又四边形ABCD是正方形,  ,
,  平面BB1D1D,
平面BB1D1D,又
 平面B1MN,
平面B1MN,  平面B1MN
平面B1MN 平面BB1D1D (6分)
平面BB1D1D (6分)
(II)设正方体棱长为2,取CD中点H,连C1H、MH,由于MH∥C1B1,MH=C1B1,所以四边形C1HM B1为平行四边形, M B1∥C1H,所以直线C1H与平面A1C1P所成角θ即为直线MB1与平面A1C1P所成角。设H到平面的距离为h,∵P为DD1中点,所以A1P=C1P=
 ,
, ,
, ,由
,由 得,h=
得,h= ,所以sinθ=
,所以sinθ= ; ( 12分)
; ( 12分)(法二)
以D为原点,DA、DC、DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,如图所示,则D(0,0,0),A(2,0,0),B(2,2,0),C(0,2,0),D1(0,0,2),A1(2,0,2),B1(2,2,2),C1(0,2,2),P(0,0,x),M(2,1,0),N(1,2,0)
(I)

 ,
, ,
, ,∴
,∴ ,
, ,
,  ,
, ,
, ,
, 平面BB1D1D,又
平面BB1D1D,又 平面B1MN,
平面B1MN,  平面B1MN
平面B1MN 平面BB1D1D (6分)
平面BB1D1D (6分)
(II)设
 为平面平面A1C1P的一个法向量,
为平面平面A1C1P的一个法向量, P为DD1中点,P(0,0,1),
P为DD1中点,P(0,0,1), ,
, ,则
,则 ,也就是
,也就是 ,
, ,令
,令 ,
, 又
又 ,设MB1与平面A1C1P所成角为θ,
,设MB1与平面A1C1P所成角为θ,则


 , ( 12分
, ( 12分
练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
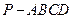 中,
中,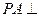 底面
底面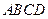 ,
,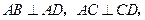
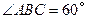 ,
,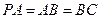 ,
,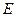 是
是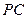 的中点.
的中点.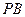 和平面
和平面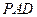 所成的角的大小;
所成的角的大小;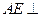 平面
平面 ;
;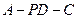 的正弦值
的正弦值
 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。 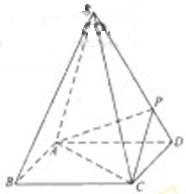
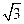 ,
,
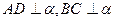 ,AD=4,
,AD=4, ,
,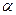 内的轨迹是 ( )
内的轨迹是 ( )
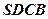 中,
中, ,
,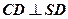 ,
,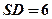 ,
,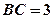 ,
,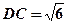 ,
,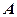 是
是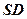 的中点,
的中点,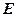 是线段
是线段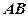 的中点,沿
的中点,沿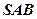 折起到平面
折起到平面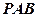 的位置,使
的位置,使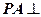 平面
平面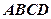 ,则下列命题正确的个数是 。
,则下列命题正确的个数是 。
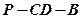 成角
成角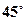 ;
;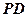 的中点
的中点 ,则
,则 平面
平面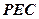 ;
;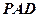 所成的锐二面角的大小为
所成的锐二面角的大小为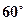 ;
; 到平面
到平面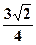
 是异面直线,
是异面直线, ,
,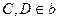 ,
,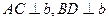 ,且
,且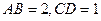 ,则
,则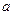 与
与 所成的角是( )
所成的角是( )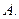


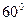


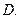
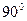
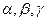 是三个不重合的平面,
是三个不重合的平面,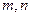 是不重合的直线,下列判断正确的是(▲ )
是不重合的直线,下列判断正确的是(▲ ) 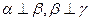 则
则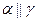
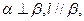 则
则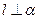
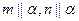 则
则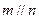
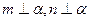 则
则