题目内容
6.关于x的方程cos2x+sin2x=2k在(0,$\frac{π}{2}$)上有两个不同的实数解,求k的取值范围.分析 令f(x)=sin2x+cos2x,g(x)=2k,问题转化为函数f(x)与g(x)的图象有两个不同的交点,由三角函数知识作出图象可得.
解答 解:令f(x)=sin2x+cos2x,g(x)=2k,
则f(x)=sin2x+cos2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$).
∵x∈(0,$\frac{π}{2}$),∴2x+$\frac{π}{4}$∈($\frac{π}{4}$,$\frac{5π}{4}$),
∴$\sqrt{2}$sin(2x+$\frac{π}{4}$)∈(-1,$\sqrt{2}$],
函数f(x)在(0,$\frac{π}{2}$)内的图象如图所示: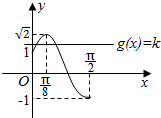
∴要使方程sin2x+cos2x=2k在区间(0,$\frac{π}{2}$)上有两个不同的实数解,
则函数f(x)与g(x)的图象有两个不同的交点,
则2k的取值范围为(1,$\sqrt{2}$).
∴k的取值范围为:($\frac{1}{2}$,$\frac{\sqrt{2}}{2}$)
点评 本题考查两角和与差的正弦函数,涉及转化思想方法和数形结合思想,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目