题目内容
7.在数列{an}中,若a1,a2-a1,a3-a2,…,an-an-1,…是首项为1,公比为$\frac{1}{2}$的等比数列,则a5=$\frac{31}{16}$.分析 直接把数列a1,a2-a1,a3-a2,…,an-an-1,…的前n项求和即可得到答案.
解答 解:由题意可知,an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=$\frac{1•[1-(\frac{1}{2})^{n}]}{1-\frac{1}{2}}$=2[1-($\frac{1}{2}$)n],
∴a5=2[1-($\frac{1}{2}$)5]=2×$\frac{31}{32}$=$\frac{31}{16}$,
故答案为:$\frac{31}{16}$
点评 本题考查了等比数列的前n项和公式,利用累加法转化为求和问题是解决本题的关键.

练习册系列答案
相关题目
18. 下图是1,2两组各7名同学体重(单位:千克)数据的茎叶图.设1,2两组数据的平均数依次为$\overline{x_1}$和$\overline{x_2}$,标准差依次为s1和s2,那么( )
下图是1,2两组各7名同学体重(单位:千克)数据的茎叶图.设1,2两组数据的平均数依次为$\overline{x_1}$和$\overline{x_2}$,标准差依次为s1和s2,那么( )
(注:标准差s=$\sqrt{\frac{1}{n}[{{({x_1}-\overline x)}^2}+{{({x_2}-\overline x)}^2}+…+{{({x_n}-\overline x)}^2}}$,其中$\overline{x_1}$为x1,x2,…,xn的平均数)
 下图是1,2两组各7名同学体重(单位:千克)数据的茎叶图.设1,2两组数据的平均数依次为$\overline{x_1}$和$\overline{x_2}$,标准差依次为s1和s2,那么( )
下图是1,2两组各7名同学体重(单位:千克)数据的茎叶图.设1,2两组数据的平均数依次为$\overline{x_1}$和$\overline{x_2}$,标准差依次为s1和s2,那么( )(注:标准差s=$\sqrt{\frac{1}{n}[{{({x_1}-\overline x)}^2}+{{({x_2}-\overline x)}^2}+…+{{({x_n}-\overline x)}^2}}$,其中$\overline{x_1}$为x1,x2,…,xn的平均数)
| A. | $\overline{x_1}$<$\overline{x_2}$,s1<s2 | B. | $\overline{x_1}$<$\overline{x_2}$,s1>s2 | C. | $\overline{x_1}$>$\overline{x_2}$,s1>s2 | D. | $\overline{x_1}$>$\overline{x_2}$,s1<s2 |
12.已知x,y满足不等式组,则$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+y≤5}\\{3x+y≤9}\end{array}\right.$,则x+2y的最大值是( )
| A. | 3 | B. | 7 | C. | 8 | D. | 10 |
19.在△ABC中,角A,B,C所对的边分别为a,b,c,设△ABC的面积为S,下列条件不能推出B≤60°的是( )
| A. | a,b,c成等比数列 | B. | a,b,c成等差数列 | C. | 1+2cos2B≥0 | D. | S≤$\frac{\sqrt{3}}{4}$(a2+c2-b2) |
16.若二项式(2x+$\frac{a}{x}$)7的展开式中$\frac{1}{{x}^{3}}$项的系数是84,则实数a=( )
| A. | 2 | B. | $\root{3}{4}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | 1 |
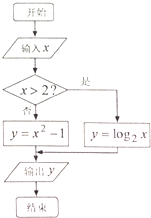 某函数的解析式由如图所示的程序框图给出.
某函数的解析式由如图所示的程序框图给出. 则下列结论正确的是( )
则下列结论正确的是( ) 是偶函数 B.
是偶函数 B. 是增函数
是增函数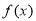 是周期函数 D.
是周期函数 D. 的值域为
的值域为