题目内容
2.已知数列{log2xn}是首项和公差均为-1的等差数列,且yn=xn2(n∈N*);(Ⅰ)求数列{xn},{yn}的通项公式xn,yn(n∈N*);
(Ⅱ)设an=$\frac{1}{{1+{x_n}}}+\frac{1}{{1-{x_{n+1}}}}$,数列{an}的前n项和为Tn.求证:Tn>2n-$\frac{1}{2}$;
(Ⅲ)设bn=1-log2yn,若对于任意正整数n,不等式$(1+\frac{1}{b_1})(1+\frac{1}{b_2})$…$(1+\frac{1}{b_n})$≥a$\sqrt{2n+3}$成立,求正数a的取值范围.
分析 (Ⅰ)由题意和等差数列的通项公式求出log2xn,利用对数的运算法则求出通项公式xn,代入式子求出yn;
(Ⅱ)把${x_n}={(\frac{1}{2})^n}$代入an=$\frac{1}{{1+{x_n}}}+\frac{1}{{1-{x_{n+1}}}}$化简,根据式子的特点进行放缩为:an$>2-(\frac{1}{{2}^{n}}-\frac{1}{{2}^{n+1}})$,利用裂项相消法证明结论成立;
(Ⅲ)把${y_n}=\frac{1}{4^n}$代入bn=1-log2yn化简,利用分离常数法化简不等式,设$f(n)=\frac{1}{\sqrt{2n+3}}(1+\frac{1}{{b}_{1}})(1+\frac{1}{{b}_{2}})…(1+\frac{1}{{b}_{n}})$,利用作商法,即化简$\frac{f(n+1)}{f(n)}$后判断出与1的关系,确定出f(n)的单调性,求出f(n)的最小值,利用恒成立问题求出正数a的取值范围.
解答 解:(Ⅰ)∵数列{log2xn}是首项和公差均为-1的等差数列,
∴log2xn=-1+(-1)(n-1)=-n,则xn=2-n=$\frac{1}{{2}^{n}}$
∴yn=xn2=$\frac{1}{{4}^{n}}$;
证明:(Ⅱ)由(I)知${x_n}={(\frac{1}{2})^n}$,
所以${a_n}=\frac{1}{{1+{{(\frac{1}{2})}^n}}}+\frac{1}{{1-{{(\frac{1}{2})}^{n+1}}}}=\frac{2^n}{{{2^n}+1}}+\frac{{{2^{n+1}}}}{{{2^{n+1}}-1}}$=$\frac{{{2^n}+1-1}}{{{2^n}+1}}$+$\frac{{{2^{n+1}}-1+1}}{{{2^{n+1}}-1}}$
=$1-\frac{1}{{{2^n}+1}}$+1+$\frac{1}{{{2^{n+1}}-1}}$=$2-(\frac{1}{{{2^n}+1}}-$$\frac{1}{{2}^{n+1}-1})$,
由$\frac{1}{{{2^n}+1}}<\frac{1}{2^n}$,$\frac{1}{{{2^{n+1}}-1}}>\frac{1}{{{2^{n+1}}}}$,得$\frac{1}{{{2^n}+1}}-$$\frac{1}{{{2^{n+1}}-1}}$$<\frac{1}{2^n}-$$\frac{1}{{{2^{n+1}}}}$,
所以an=$2-(\frac{1}{{{2^n}+1}}-$$\frac{1}{{2}^{n+1}-1})$$>2-(\frac{1}{2^n}-$$\frac{1}{{2}^{n+1}})$
则${T_n}={a_1}+{a_2}+…+{a_n}>[2-(\frac{1}{2}-\frac{1}{2^2})]+[2-(\frac{1}{2^2}-\frac{1}{2^3})]+…+[2-(\frac{1}{2^n}-\frac{1}{{{2^{n+1}}}})]$
=$2n-[(\frac{1}{2}-\frac{1}{2^2})+(\frac{1}{2^2}-\frac{1}{2^3})]+…+(\frac{1}{2^n}-\frac{1}{{{2^{n+1}}}})]$=$2n-(\frac{1}{2}-\frac{1}{{{2^{n+1}}}})>2n-\frac{1}{2}$,
即Tn>$2n-\frac{1}{2}$.
解:(Ⅲ)由${y_n}=\frac{1}{4^n}$,得bn=2n+1.
对任意正整数n,不等式$(1+\frac{1}{{b}_{1}})(1+\frac{1}{{b}_{2}})•…•(1+\frac{1}{{b}_{n}})≥a\sqrt{2n+3}$成立,
即$a≤\frac{1}{{\sqrt{2n+3}}}$$(1+\frac{1}{{b}_{1}})(1+\frac{1}{{b}_{2}})•…•(1+\frac{1}{{b}_{n}})$恒成立.
设$f(n)=\frac{1}{{\sqrt{2n+3}}}$$(1+\frac{1}{{b}_{1}})(1+\frac{1}{{b}_{2}})•…•(1+\frac{1}{{b}_{n}})$,
则$f(n+1)=\frac{1}{\sqrt{2n+5}}$$(1+\frac{1}{{b}_{1}})(1+\frac{1}{{b}_{2}})•…•(1+\frac{1}{{b}_{n}})$$(1+\frac{1}{{b}_{n+1}})$
所以$\frac{f(n+1)}{f(n)}$=$\frac{\sqrt{2n+3}}{\sqrt{2n+5}}$•$(1+\frac{1}{{b}_{n+1}})$=$\frac{\sqrt{2n+3}}{\sqrt{2n+5}}$$•\frac{2n+4}{2n+3}$=$\frac{2n+4}{\sqrt{2n+5}\sqrt{2n+3}}$
=$\frac{\sqrt{4{n}^{2}+16n+16}}{\sqrt{4{n}^{2}+16n+15}}$>1,
所以f(n+1)>f(n),则f(n)单调递增,
则f(n)的最小值是f(1)=$\frac{1}{\sqrt{5}}×\frac{4}{3}$=$\frac{4\sqrt{5}}{15}$,
所正数a的取值范围是$(0,\frac{4\sqrt{5}}{15}]$.
点评 本题考查等差数列的通项公式,数列与不等式、函数结合的问题,考查放缩法,分离常数法,作商法等,考查分析、解决问题的能力,属于难题.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案| A. | [-2,+∞) | B. | (-2,+∞) | C. | [-3,+∞) | D. | (-3,+∞) |
| A. | (a-1)(c-1)>0 | B. | ac>1 | C. | ac=1 | D. | ac<1 |
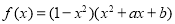 的图象关于直线
的图象关于直线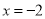 对称,则
对称,则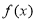 的最大值为 .
的最大值为 .