Question

【题目】已知过双曲线C： =1（a＞0，b＞0）的中心的直线交双曲线于点A，B，在双曲线C上任取与点A，B不重合的点P，记直线PA，PB，AB的斜率分别为k1 ， k2 ， k，若k1k2＞k恒成立，则离心率e的取值范围为（ ）
A.1＜e＜
B.1＜e≤
C.e＞
D.e≥

Answer 1

【答案】D
【解析】解：设A（x1 ， y1），P（x2 ， y2），
由题意知点A，B为过原点的直线与双曲线 =1的交点，
∴由双曲线的对称性得A，B关于原点对称，
∴B（﹣x1 ， ﹣y1），
∴k1k2= = ，
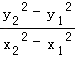∵点A，P都在双曲线上，
∴ ﹣ =1， ﹣ =1，
两式相减，可得： = ，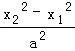
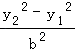即有k1k2= ，又k= ，
由双曲线的渐近线方程为y=± x，则k趋近于 ，
k1k2＞k恒成立，则 ≥ ，
即有b≥a，即b2≥a2 ，
即有c2≥2a2 ，
则e= ≥ ．
故选D．