题目内容
【题目】已知正项等差数列{an}的前n项和为Sn , 且满足 ![]() ,S7=56. (Ⅰ)求数列{an}的通项公式an;
,S7=56. (Ⅰ)求数列{an}的通项公式an;
(Ⅱ)若数列{bn}满足b1=a1且bn+1﹣bn=an+1 , 求数列 ![]() 的前n项和Tn .
的前n项和Tn .
【答案】解:(Ⅰ)∵{an}是等差数列且 ![]() , ∴
, ∴ ![]() ,
,
又∵an>0∴a3=6.
∵ ![]() ,
,
∴d=a4﹣a3=2,
∴an=a3+(n﹣3)d=2n.
(Ⅱ)∵bn+1﹣bn=an+1且an=2n,
∴bn+1﹣bn=2(n+1)
当n≥2时,bn=(bn﹣bn﹣1)+(bn﹣1﹣bn﹣2)+…+(b2﹣b1)+b1
=2n+2(n﹣1)+…+2×2+2=n(n+1),
当n=1时,b1=2满足上式,bn=n(n+1)
∴ ![]()
∴ ![]()
= ![]()
【解析】(Ⅰ)由已知可得 ![]() ,可求a3 , 利用等差数列的求和公式及性质可求a4 , 则d=a4﹣a3 , 从而可求通项(Ⅱ)由已知可得bn+1﹣bn=2(n+1),利用叠加法可求bn , 然后利用裂项相消法可求数列的和
,可求a3 , 利用等差数列的求和公式及性质可求a4 , 则d=a4﹣a3 , 从而可求通项(Ⅱ)由已知可得bn+1﹣bn=2(n+1),利用叠加法可求bn , 然后利用裂项相消法可求数列的和
【考点精析】本题主要考查了等差数列的通项公式(及其变式)和数列的前n项和的相关知识点,需要掌握通项公式:![]() 或
或![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系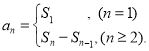 才能正确解答此题.
才能正确解答此题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目