题目内容
若 为两条异面直线,
为两条异面直线, 为其公垂线,直线
为其公垂线,直线 ,则
,则 与
与 两直线的交
两直线的交
点个数为( )
 为两条异面直线,
为两条异面直线, 为其公垂线,直线
为其公垂线,直线 ,则
,则 与
与 两直线的交
两直线的交点个数为( )
| A.0个 | B.1个 | C.最多1个 | D.最多2个 |
C
由空间中线线的位置关系知,空间中线线位置关系有三种,相交,平行,异面,
由题设条件AB是异面直线a,b的公垂线,直线l∥AB知,
l与两直线a,b可能是异面的,此时有0个交点,
l与两直线a,b可能相交,但至多与其中一个直线相交,这是因为直线l∥EF,它们可以确定一个平面γ,若l与a,b同时有交点,此两交点必在γ上,这就使得两异面直线上各有两个点在γ上,此时两异面直线不现异面,故l与a,b不能有两个交点,
综上知,l与a,b交点的个数是0个或1个,应选C。
由题设条件AB是异面直线a,b的公垂线,直线l∥AB知,
l与两直线a,b可能是异面的,此时有0个交点,
l与两直线a,b可能相交,但至多与其中一个直线相交,这是因为直线l∥EF,它们可以确定一个平面γ,若l与a,b同时有交点,此两交点必在γ上,这就使得两异面直线上各有两个点在γ上,此时两异面直线不现异面,故l与a,b不能有两个交点,
综上知,l与a,b交点的个数是0个或1个,应选C。

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 、
、 ,下列命题中正确的是( )
,下列命题中正确的是( )
 ,则
,则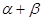 满足( )
满足( )



 )
)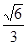 )
)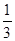 )
) )
) 的角,
的角, ,则OP与平面AOB所成的角等于( )
,则OP与平面AOB所成的角等于( )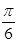 B.
B. D.
D.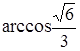

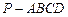 中,
中,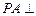 平面
平面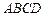 ,底面
,底面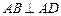 ,
,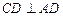 。
。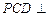 平面
平面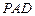 ;
;
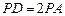 ,求二面角
,求二面角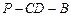 的大小。
的大小。 底面ABCD,M,N分别PA,BC的中点,且PD="AD=1" (12分)
底面ABCD,M,N分别PA,BC的中点,且PD="AD=1" (12分)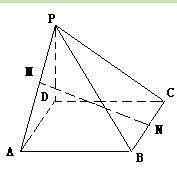
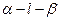 为
为 ,
, 是棱
是棱 上的两点,
上的两点, 分别在半平面
分别在半平面 内,
内, ,则
,则 长为
长为