题目内容
等差数列{an}的前n项和为Sn,已知S10=0,S15 =25,则nSn的最小值为 ( )
| A.-48 |
| B.-40 |
| C.-49 |
| D.-43 |
C
∵数列{an}是等差数列
∴2a1+9d=0,3a1+21d=5,解之得a1=-3,d=
∴nSn= n3-
n3- n2
n2
设f(x)= x3-
x3- x2(x∈N+),则f′(x)= x2-
x2(x∈N+),则f′(x)= x2- x
x
∴当x∈(-∞,0)及( ,+∞)时, f(x)为增函数;
,+∞)时, f(x)为增函数;
当x∈(0, )时,f(x)为减函数
)时,f(x)为减函数
∴当x= 时,f(x)有最小值
时,f(x)有最小值
∵x∈N+,∴n=7时,f(7)min=-49
∴2a1+9d=0,3a1+21d=5,解之得a1=-3,d=

∴nSn=
 n3-
n3- n2
n2设f(x)=
 x3-
x3- x2(x∈N+),则f′(x)= x2-
x2(x∈N+),则f′(x)= x2- x
x∴当x∈(-∞,0)及(
 ,+∞)时, f(x)为增函数;
,+∞)时, f(x)为增函数;当x∈(0,
 )时,f(x)为减函数
)时,f(x)为减函数∴当x=
 时,f(x)有最小值
时,f(x)有最小值∵x∈N+,∴n=7时,f(7)min=-49

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 是等差数列,
是等差数列, 是等比数列,其中
是等比数列,其中 ,
, ,且
,且 为
为 、
、 的等差中项,
的等差中项, 的等差中项.
的等差中项. ,求数列
,求数列 的前
的前 项和
项和 .
. 的前
的前 项和为
项和为 .已知
.已知 ,
, =an+1-
=an+1- n2-n-
n2-n- (
( )
) 的值;
的值; +
+ +…+
+…+ <
< .
. 满足:对任意
满足:对任意 ,有
,有 .记
.记 .
. ,公比
,公比 的等比数列,求数列
的等比数列,求数列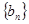 的通项公式;
的通项公式; ,证明:
,证明: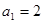 ;
; ,
, 是公差为1的等差数列.记
是公差为1的等差数列.记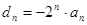 ,
, ,问:使
,问:使 成立的最小正整数
成立的最小正整数 是否存在?并说明理由.
是否存在?并说明理由. 是等差数列,且
是等差数列,且 且
且 成等比数列。
成等比数列。 ,求前n项和
,求前n项和 .
. 的公差
的公差 大于0,
大于0, 是方程
是方程 的两根.
的两根.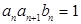 ,求数列
,求数列 的前
的前 项和.
项和. 的前n项和为
的前n项和为 ,若
,若 ,则
,则 =__________。
=__________。 中,
中,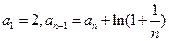 ,则
,则 =( )
=( )


