题目内容
设数列 是等差数列,且
是等差数列,且 且
且 成等比数列。
成等比数列。
(1).求数列 的通项公式
的通项公式
(2).设 ,求前n项和
,求前n项和 .
.
 是等差数列,且
是等差数列,且 且
且 成等比数列。
成等比数列。(1).求数列
 的通项公式
的通项公式(2).设
 ,求前n项和
,求前n项和 .
.(1)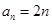 ;(2)
;(2)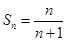 .
.
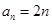 ;(2)
;(2)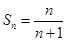 .
.试题分析:本题主要考查等差数列的通项公式、数列求和、解方程等基础知识,意在考查考生的运算求解能力、基本量思想和利用裂项相消法的解题能力.第一问,利用等比中项将数学语言写成数学表达式,再利用等差数列的通项公式将
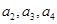 展开,通过解方程,解出基本量
展开,通过解方程,解出基本量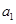 和
和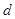 ,而此题
,而此题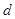 有2个值,需通过已知条件验证舍掉一个,从而得到等差数列的通项公式;第二问,利用第一问的结论,代入到
有2个值,需通过已知条件验证舍掉一个,从而得到等差数列的通项公式;第二问,利用第一问的结论,代入到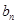 中,用裂项相消法求和.
中,用裂项相消法求和.试题解析:(1)设等差数列
 的公差为
的公差为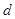 ,又
,又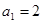
则
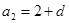 ,
,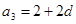 ,
,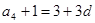 ,
,又
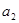 ,
,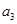 ,
,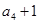 成等比数列.
成等比数列.∴
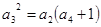 ,即
,即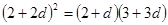 ,
,解得
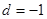 或
或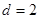 , 4分
, 4分又
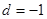 时,
时,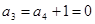 ,与
,与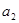 ,
,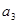 ,
,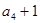 成等比数列矛盾,
成等比数列矛盾,∴
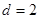 ,∴
,∴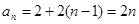 ,即
,即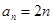 . 6分
. 6分(2)因为
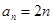 ,∴
,∴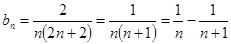 8分
8分∴
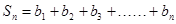
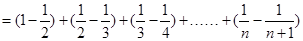
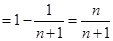 .
.12分

练习册系列答案
相关题目
 满足
满足 (
( ).
). 的值;
的值; (用含
(用含 的式子表示);
的式子表示); ,数列
,数列
 的前
的前 ,求
,求 )项,且
)项,且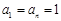 ,对每个i (1≤i≤
,对每个i (1≤i≤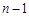 ,i
,i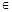 N),均有
N),均有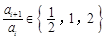 .
.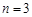 时,写出满足条件的所有数列{an}(不必写出过程);
时,写出满足条件的所有数列{an}(不必写出过程);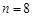 时,求满足条件的数列{an}的个数.
时,求满足条件的数列{an}的个数. 中,已知
中,已知 .
. 分别为等差数列
分别为等差数列 的第3项和第5项,试求数列
的第3项和第5项,试求数列 项和
项和 。
。 间的整数
间的整数 为分子,以
为分子,以 为分母组成分数集合
为分母组成分数集合 ,其所有元素和为
,其所有元素和为 ;以
;以 间的整数
间的整数 为分母组成不属于集合
为分母组成不属于集合 ,其所有元素和为
,其所有元素和为 ;……,依次类推以
;……,依次类推以 间的整数
间的整数 为分母组成不属于
为分母组成不属于 的分数集合
的分数集合 ,其所有元素和为
,其所有元素和为 ;则
;则 =________.
=________.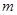 行:
行: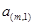
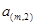
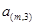
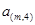
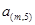 ………………
………………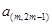
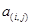 表示第
表示第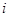 行中的第
行中的第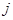 个数)
个数)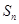 是等差数列
是等差数列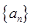 的前
的前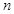 项和,公差
项和,公差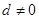 ,若
,若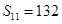 ,若
,若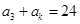 ,则正整数
,则正整数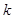 的值为( )
的值为( )



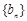 为等差数列,
为等差数列,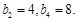 数列
数列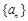 满足
满足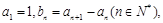 则
则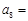 ( )
( )