题目内容
已知数列 是等差数列,
是等差数列, 是等比数列,其中
是等比数列,其中 ,
, ,且
,且 为
为 、
、 的等差中项,
的等差中项, 为
为 、
、 的等差中项.
的等差中项.
(1)求数列 与
与 的通项公式;
的通项公式;
(2)记 ,求数列
,求数列 的前
的前 项和
项和 .
.
 是等差数列,
是等差数列, 是等比数列,其中
是等比数列,其中 ,
, ,且
,且 为
为 、
、 的等差中项,
的等差中项, 为
为 、
、 的等差中项.
的等差中项.(1)求数列
 与
与 的通项公式;
的通项公式;(2)记
 ,求数列
,求数列 的前
的前 项和
项和 .
.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)确定等差数列和等比数列各需两个独立条件,由已知得,
 ,且
,且 ,故联立求
,故联立求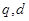 ,则数列
,则数列 与
与 的通项公式可求;(2)求数列的前n项和,首先应考虑通项公式,根据通项公式的不同特点选择相应的求和方式.本题先分别求等差数列和等比数列的前n项和,代入
的通项公式可求;(2)求数列的前n项和,首先应考虑通项公式,根据通项公式的不同特点选择相应的求和方式.本题先分别求等差数列和等比数列的前n项和,代入 中,求得
中,求得 ,则
,则 ,分别利用错位相减法和等差数列前n项和公式计算即可.
,分别利用错位相减法和等差数列前n项和公式计算即可.试题解析:(1)设公比及公差分别为
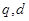
由
 得
得 或
或 , 3分
, 3分又由
 ,故
,故 4分
4分从而
 6分
6分(2)
 8分
8分 9分
9分令
 ①
① ②
②由②—①得
 11分
11分∴
 12分
12分
练习册系列答案
相关题目
 ,
, ,且
,且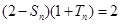 ,
, .
. ,证明数列{bn}是等比数列;
,证明数列{bn}是等比数列; ,求集合
,求集合 .
.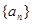 的前n项和为Sn,且满足
的前n项和为Sn,且满足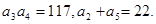
 的前n项和为
的前n项和为 ,则
,则 = .
= .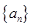 满足条件
满足条件 , 则
, 则 .
.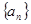 是等差数列,且
是等差数列,且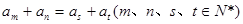 ,
,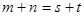 ;
;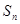 是等差数列
是等差数列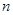 项的和,则
项的和,则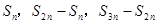 成等差数列;
成等差数列;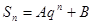 ;(其中
;(其中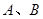 是非零常数,
是非零常数,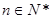 ),则
),则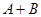 为零.
为零. 间的整数
间的整数 为分子,以
为分子,以 为分母组成分数集合
为分母组成分数集合 ,其所有元素和为
,其所有元素和为 ;以
;以 间的整数
间的整数 为分母组成不属于集合
为分母组成不属于集合 ,其所有元素和为
,其所有元素和为 ;……,依次类推以
;……,依次类推以 间的整数
间的整数 为分母组成不属于
为分母组成不属于 的分数集合
的分数集合 ,其所有元素和为
,其所有元素和为 ;则
;则 =________.
=________. 中,
中, 的值是
的值是