题目内容
【题目】在平面直角坐标系![]() 中,设椭圆
中,设椭圆![]() 的左焦点为
的左焦点为![]() ,左准线为
,左准线为![]() 为椭圆
为椭圆![]() 上任意一点,直线
上任意一点,直线![]() ,垂足为
,垂足为![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() .
.

(1)若![]() ,且
,且![]() ,直线
,直线![]() 的方程为
的方程为![]() .①求椭圆
.①求椭圆![]() 的方程;②是否存在点
的方程;②是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 两点,求证:直线
两点,求证:直线![]() 均与圆
均与圆![]() 相切.
相切.
【答案】(1)①![]() ;②不存在;(2)证明见解析.
;②不存在;(2)证明见解析.
【解析】
(1)①根据左准线方程求出参数a,从而得出椭圆方程;
②设出![]() ,根据点
,根据点![]() 在椭圆上且
在椭圆上且![]() 得出关于
得出关于![]() 的方程组,根据
的方程组,根据![]() 解的情况,得出结果;
解的情况,得出结果;
(2)设点![]() ,
,![]() ,根据
,根据![]() ,求出
,求出![]() ,对
,对![]() 进行转化,借助
进行转化,借助![]() 在圆
在圆![]() 上,进而得出结果.
上,进而得出结果.
解:(1)①因为直线![]() 的方程为
的方程为![]() ,
,
所以![]()
因为![]() ,
,
所以![]() ,解得
,解得![]() 或
或![]()
因为![]() ,
,
所以![]() ,
,![]() ,
,
椭圆方程为![]() .
.
②设![]() ,则
,则![]() ,即
,即![]() ,
,
当![]() 或
或![]() 时,均不符合题意;
时,均不符合题意;
当![]() 或
或![]() 时,直线
时,直线![]() 的斜率为
的斜率为![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
故直线![]() 的方程为
的方程为![]() ,
,
联立方程组 ,解得
,解得![]() ,
,
所以 ,
,
因为![]() ,
,
故![]() ,
,
即![]() 或
或![]()
方程![]() 的根为
的根为![]() ,
,
因为![]() ,故无解;
,故无解;
方程![]() 的
的![]() ,故无解,
,故无解,
综上:不存在点P使![]() .
.
(2)设![]() ,
,![]()
则![]() ,
,![]() ,
,
因为![]() ,
,
所以![]() ,
,
即![]() ,
,
由题意得![]() ,所以
,所以![]() ,
,
所以![]()
因为![]() ,
,![]()
所以![]()
![]()
![]()
![]()
因为![]() 在圆
在圆![]() 上,所以
上,所以![]() ,即
,即![]() ,
,
故![]() ,
,
所以![]() ,
,
所以直线![]() 与圆
与圆![]() 相切,
相切,
同理可证:![]() 与圆
与圆![]() 相切.
相切.

练习册系列答案
相关题目
【题目】某高校在2017年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如表:
组号 | 分组 | 频率 |
第1组 |
|
|
第2组 |
|
|
第3组 |
|
|
第4组 |
|
|
第5组 |
|
|
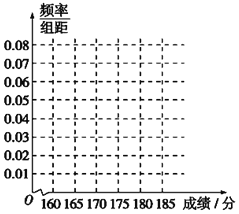
![]() 求出频率分布表中
求出频率分布表中![]() 处应填写的数据,并完成如图所示的频率分布直方图;
处应填写的数据,并完成如图所示的频率分布直方图;
![]() 根据直方图估计这次自主招生考试笔试成绩的平均数和中位数
根据直方图估计这次自主招生考试笔试成绩的平均数和中位数![]() 结果都保留两位小数
结果都保留两位小数![]() .
.





