题目内容
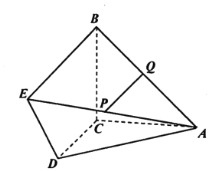
【题目】如图,在五棱锥P-ABCDE中,△ABE是等边三角形,四边形BCDE是直角梯形且∠DEB=∠CBE=90°,G是CD的中点,点P在底面的射影落在线段AG上.
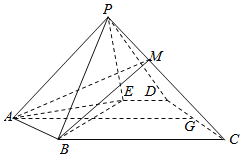
(Ⅰ)求证:平面PBE⊥平面APG;
(Ⅱ)已知AB=2,BC=![]() ,侧棱PA与底面ABCDE所成角为45°,S△PBE=
,侧棱PA与底面ABCDE所成角为45°,S△PBE=![]() ,点M在侧棱PC上,CM=2MP,求二面角M-AB-D的余弦值.
,点M在侧棱PC上,CM=2MP,求二面角M-AB-D的余弦值.
【答案】(I)见解析; (II)![]() .
.
【解析】
(Ⅰ)由题易证BE⊥PO,BE⊥AG,可得BE⊥平面PAG,既而证得平面PBE⊥平面APG;
(II)建立空间直角坐标系,分别求出平面MAB和平面ABD的法向量,再根据二面角的公式求得二面角M-AB-D的余弦值即可.
(Ⅰ)取BE中点F,连接AF,GF,由题意得A,F,G三点共线,
过点P作PO⊥AG于O,则PO⊥底面ABCDE
∵BE平面ABCDE,∴BE⊥PO,
∵△ABE是等边三角形,
∴BE⊥AG
∵AG∩PO=O,∴BE⊥平面PAG,
∵BE平面PBE,
∴平面PBE⊥平面APG.
(II)连接PF,∵![]()
又∵∠PAF=45°,∴PF⊥AF,∴PF⊥AF,
∴PF⊥底面ABCDE.
∴O点与F点重合.
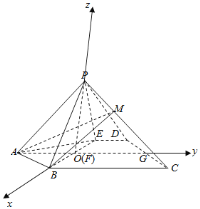
如图,以O为原点,分别以![]() 的方向为x轴,y轴,z轴正方向,建立空间直角坐标系.
的方向为x轴,y轴,z轴正方向,建立空间直角坐标系.
底面ABCDE的一个法向量![]()
∵![]() ,∴
,∴![]() ,
,
设平面ABM的法向量![]() ,
,
∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴ ,取
,取![]() 则
则![]() ,
,
∴![]() ,
,
∵二面角的法向量![]() 分别指向二面角的内外,<
分别指向二面角的内外,<![]() >即为二面角的平面角,
>即为二面角的平面角,
∴cos<![]() >
>![]() =
=![]() =
=![]() .
.
∴二面角M-AB-D的余弦值为![]() .
.
)

练习册系列答案
相关题目