题目内容
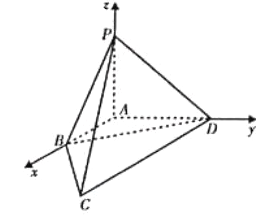
【题目】如图，在四棱锥
中，已知棱
，
，
两两垂直，长度分别为1，2，2.若
（
），且向量
与
夹角的余弦值为
.
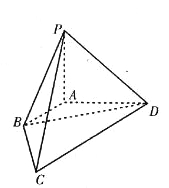
（1）求
的值；
（2）求直线
与平面
所成角的正弦值.
【答案】（1）
；（2）
.
【解析】
试题（1）以
为坐标原点，
、
、
分别为
、
、
轴建立空间直角坐标系
，写出
，
的坐标，根据空间向量夹角余弦公式列出关于
的方程可求；（2）设岀平面
的法向量为
，根据
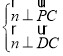，进而得到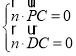
，从而求出
，向量
的坐标可以求出，从而可根据向量夹角余弦的公式求出
，从而得
和平面
所成角的正弦值.
试题解析：（1）依题意，以为坐标原点，、、分别为、、轴建立空间直角坐标系
，因为
，所以
，从而
，则由
，解得
（舍去）或.
（2）易得
，
，设平面
的法向量
，
则
，
，即
，且
，所以
，不妨取
，则平面的一个法向量
，又易得
，故
，所以直线
与平面所成角的正弦值为.
考点: 1、空间两向量夹角余弦公式；2、利用向量求直线和平面说成角的正弦.
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
【题目】有人认为在机动车驾驶技术上，男性优于女性.这是真的么？某社会调查机构与交警合作随机统计了经常开车的
名驾驶员最近三个月内是否有交通事故或交通违法事件发生，得到下面的列联表：
男 | 女 | 合计 | |
无 | 40 | 35 | 75 |
有 | 15 | 10 | 25 |
合计 | 55 | 45 | 100 |
附：
.
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
据此表，可得
A. 认为机动车驾驶技术与性别有关的可靠性不足
B. 认为机动车驾驶技术与性别有关的可靠性超过
C. 认为机动车驾驶技术与性别有关的可靠性不足
D. 认为机动车驾驶技术与性别有关的可靠性超过
