题目内容
10.已知等比数列{an}的前n项和为Sn,且满足Sn =2n+1+2p(n∈N*).(1)求p的值及数列{an}的通项公式;
(2)若数列{bn}满足$\frac{{a}_{n+1}}{2}$=(3+p)${\;}^{{a}_{n}{b}_{n}}$.求数列{bn}的前n项和Tn.
分析 (1)通过Sn =2n+1+2p可知a1=4+2p、a2=4、a3=8,利用${{a}_{2}}^{2}={a}_{1}{a}_{3}$可知p=-1,进而可知首项、公比,计算即得结论;
(2)通过(1)可知$\frac{{a}_{n+1}}{2}$=(3+p)${\;}^{{a}_{n}{b}_{n}}$可化简为2n=${2}^{{a}_{n}{b}_{n}}$,进而可知bn=$\frac{n}{{2}^{n}}$,利用错位相减法计算即得结论.
解答 解:(1)∵Sn =2n+1+2p,
∴a1=4+2p,a2=S2-S1=4,a3=S3-S2=8,
又∵数列{an}为等比数列,
∴${{a}_{2}}^{2}={a}_{1}{a}_{3}$,即16=32+16p,
解得:p=-1,
∴a1=4+2p=4-2=2,公比q=$\frac{{a}_{3}}{{a}_{2}}$=$\frac{8}{4}$=2,
∴数列{an}的通项公式an=2n;
(2)由(1)可知p=-1,$\frac{{a}_{n+1}}{2}$=2n,
∵$\frac{{a}_{n+1}}{2}$=(3+p)${\;}^{{a}_{n}{b}_{n}}$,
∴2n=${2}^{{a}_{n}{b}_{n}}$,
∴n=anbn,
∴bn=$\frac{n}{{a}_{n}}$=$\frac{n}{{2}^{n}}$,
∴Tn=1•$\frac{1}{2}$+2•$\frac{1}{{2}^{2}}$+…+n•$\frac{1}{{2}^{n}}$,
$\frac{1}{2}$Tn=1•$\frac{1}{{2}^{2}}$+2•$\frac{1}{{2}^{3}}$+…+(n-1)•$\frac{1}{{2}^{n}}$+n•$\frac{1}{{2}^{n+1}}$,
两式相减得:$\frac{1}{2}$Tn=$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}$-n•$\frac{1}{{2}^{n+1}}$,
∴Tn=1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n-1}}$-n•$\frac{1}{{2}^{n}}$
=$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$-n•$\frac{1}{{2}^{n}}$
=2-$\frac{n+2}{{2}^{n}}$.
点评 本题考查数列的通项及前n项和,考查错位相减法,注意解题方法的积累,属于中档题.

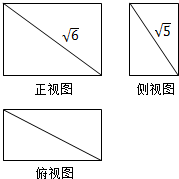 某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的长度为$\sqrt{6}$,在侧视图中的长度为$\sqrt{5}$,则该长方体的表面积为3+4$\sqrt{11}$.
某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的长度为$\sqrt{6}$,在侧视图中的长度为$\sqrt{5}$,则该长方体的表面积为3+4$\sqrt{11}$.