题目内容
已知函数f(x)是(-∞,+∞)上的增函数,a,b∈R.
(1)若a+b≥0,求证:f(a)+f(b)≥f(-a)+f(-b);
(2)判断(1)中命题的逆命题是否成立,并证明你的结论.
(1) 证明:∵a+b≥0,∴a≥-b. 由f(x)的单调性得f(a)≥f(-b) 又a+b≥0⇒b≥-a⇒f(b)≥f(-a) 两式相加即得:f(a)+f(b)≥f(-a)+f(-b) (2) 逆命题成立,假设a+b<0,那么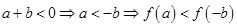 ,
,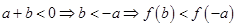 ⇒f(a)+f(b)<f(-a)+f(-b) 这与已知矛盾,故只有a+b≥0
⇒f(a)+f(b)<f(-a)+f(-b) 这与已知矛盾,故只有a+b≥0
解析试题分析:(1)证明:∵a+b≥0,∴a≥-b. 2分
由已知f(x)的单调性得f(a)≥f(-b).
又a+b≥0⇒b≥-a⇒f(b)≥f(-a). 4分
两式相加即得:f(a)+f(b)≥f(-a)+f(-b). 6分
(2)逆命题:
f(a)+f(b)≥f(-a)+f(-b)⇒a+b≥0. 8分
下面用反证法证之.
假设a+b<0,那么: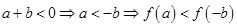
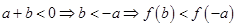
⇒f(a)+f(b)<f(-a)+f(-b). 10分
这与已知矛盾,故只有a+b≥0.逆命题得证. 12分
考点:函数单调性与反证法
点评:单调性的定义:在定义域的某个区间上,若有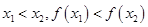 则函数为增函数,若有
则函数为增函数,若有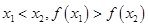 则函数为减函数;反证法证明的大体步骤:假设要证明的结论反面成立,借此推出与已知或定理发生矛盾,推翻假设肯定原结论成立
则函数为减函数;反证法证明的大体步骤:假设要证明的结论反面成立,借此推出与已知或定理发生矛盾,推翻假设肯定原结论成立

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. ,求
,求 在
在 处的切线方程;
处的切线方程; 上的最小值.
上的最小值. ,其中
,其中 为实数;
为实数; 时,试讨论函数
时,试讨论函数 的零点的个数;
的零点的个数; 对任意
对任意 都成立,求实数
都成立,求实数 的取值范围。
的取值范围。 ,
,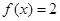 ,求
,求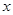 的值;
的值;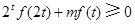 对于
对于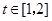 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。 的递增区间是
的递增区间是
 的值。
的值。 ,求
,求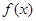 在区间
在区间 上的最大值和最小值。
上的最大值和最小值。 定义在
定义在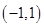 上,对于任意的
上,对于任意的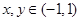 ,有
,有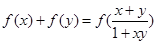 ,且当
,且当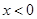 时,
时,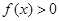 .
.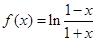 是否满足这些条件;
是否满足这些条件;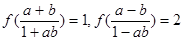 ,且
,且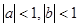 ,求
,求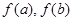 的值.
的值.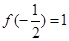 ,试解关于
,试解关于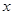 的方程
的方程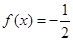 .
.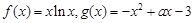 .
.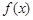 在
在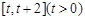 上的最小值;
上的最小值;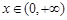 ,
,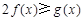 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;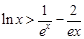 成立.
成立.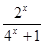 .
. 的图像相交于点A(a,2),将直线l1向上平移3个单位得到的直线l2与双曲线相交于B、C两点(点B在第一象限),与y轴交于点D.
的图像相交于点A(a,2),将直线l1向上平移3个单位得到的直线l2与双曲线相交于B、C两点(点B在第一象限),与y轴交于点D.