题目内容
4.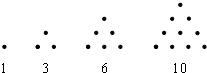 传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数.他们研究过如图的三角形数:
传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数.他们研究过如图的三角形数:将三角形数1,3,6,10,…记为数列{an},将可被5整除的三角形数按从小到大的顺序组成一个新数列
{bn},可以推测:
(Ⅰ)b2014是数列{an}中的第5035项;
(Ⅱ) b2n-1=$\frac{1}{2}$5n(5n-1).(用n表示)
分析 先归纳出数列an=$\frac{n(n+1)}{2}$,然后写出:
b1=a4,b2=a5,
b3=a9,b4=a10,
b5=a14,b6=a15,
…
再归纳出b2n=a5n,b2n-1=a5n-1.
解答 解:显然an=$\frac{n(n+1)}{2}$,数列an中是5的倍数要么n+1是5的倍数,要么n是5的倍数,
b1=a4,b2=a5,
b3=a9,b4=a10,
b5=a14,b6=a15,
…
∴b2n=a5n,b2n-1=a5n-1,
∴b2014是数列{an}中的第2014÷2×5=5035项.
∴b2n-1=$\frac{5n(5n-1)}{2}$.
点评 本题主要考查归纳推理的思维能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列命题的说法错误的是( )
| A. | 对于命题p:?x∈R,x2+x+1>0 则¬p:?x∈R,x2+x+1≤0 | |
| B. | 命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” | |
| C. | 若复合命题p∨q为假命题,则p,q都是假命题 | |
| D. | “y<2”是“向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-2,y-4)之间的夹角为钝角”的充要条件 |
12.某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品.从两个分厂生产的零件中个抽出500 件,量其内径尺寸的结果如下表(表1为甲厂,表2为乙 厂):
表1
表2
(1)试分别估计两个分厂生产的零件的优质品率;
(2)由于以上统计数据填下面2×2列联表(填写在答题卡的2×2列联表中),并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.
表1
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
(2)由于以上统计数据填下面2×2列联表(填写在答题卡的2×2列联表中),并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.
13.函数y=x4(2-x2)(0<x<$\sqrt{2}$)的最大值是( )
| A. | 0 | B. | 1 | C. | $\frac{16}{27}$ | D. | $\frac{32}{27}$ |
14.已知α,β∈($\frac{3π}{2}$,2π),满足tan(α+β)-2tanβ=0,则tanα的最小值是( )
| A. | $\frac{{3\sqrt{2}}}{4}$ | B. | -$\frac{{\sqrt{2}}}{4}$ | C. | -$\frac{{3\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{2}}}{4}$ |