题目内容
【题目】已知![]() 、
、![]() 分别是离心率为
分别是离心率为![]() 的椭圆
的椭圆![]() :
:![]() 的左、右焦点,点
的左、右焦点,点![]() 是椭圆
是椭圆![]() 上异于其左、右顶点的任意一点,过右焦点
上异于其左、右顶点的任意一点,过右焦点![]() 作
作![]() 的外角平分线
的外角平分线![]() 的垂线
的垂线![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() (
(![]() 为坐标原点).
为坐标原点).
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 在圆
在圆![]() 上,且在第一象限,过
上,且在第一象限,过![]() 作圆
作圆![]() 的切线交椭圆于
的切线交椭圆于![]() 、
、![]() 两点,问:
两点,问:![]() 的周长是否为定值?如果是,求出该定值;如果不是,说明理由.
的周长是否为定值?如果是,求出该定值;如果不是,说明理由.
【答案】(1)![]() ;(2)6.
;(2)6.
【解析】试题分析:(1)由已知条件求出![]() ,再由离心率
,再由离心率![]() ,求出b的值,写出椭圆方程;(2)设
,求出b的值,写出椭圆方程;(2)设![]() 的方程为
的方程为![]() (
(![]() ,
,![]() ),由直线AB与圆
),由直线AB与圆![]() 相切,求得
相切,求得
![]() ,设
,设![]()
![]() ,
,![]() (
(![]() ),联立直线与椭圆方程,消去y得到一个关于x的一元二次方程,求出
),联立直线与椭圆方程,消去y得到一个关于x的一元二次方程,求出![]() 的值,再算出弦长
的值,再算出弦长![]() 的表达式,由两点间的距离公式算出
的表达式,由两点间的距离公式算出![]() 的表达式,算出
的表达式,算出![]() 的周长为定值。
的周长为定值。
试题解析:(1)延长![]() 交直线
交直线![]() 于点
于点![]() ,
,
∵![]() 为
为![]() 的外角平分线的垂线,∴
的外角平分线的垂线,∴![]() ,
,![]() 为
为![]() 的中点,
的中点,
∴![]()
![]() ,
,
由椭圆的离心率![]() ,得
,得![]() ,
,![]() ,
,
∴椭圆的方程为![]() .
.
(2)由题意,设![]() 的方程为
的方程为![]() (
(![]() ,
,![]() ),
),
∵直线![]() 与圆
与圆![]() 相切,∴
相切,∴![]() ,即
,即![]() ,
,
由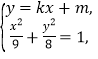 得
得![]() ,
,
设![]()
![]() ,
,![]() (
(![]() ),则
),则![]() ,
,![]() ,
,
![]()
![]()
![]()
![]() ,
,
又![]() ,
,
∴![]() ,
,
同理![]() ,
,
∴![]()
![]() ,
,
∴![]() ,即
,即![]() 的周长为定值6.
的周长为定值6.

 文敬图书课时先锋系列答案
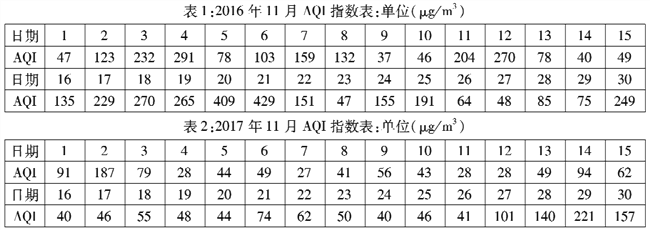
文敬图书课时先锋系列答案【题目】按照国家质量标准:某种工业产品的质量指标值落在[100,120)内,则为合格品,否则为不合格品.某企业有甲乙两套设备生产这种产品,为了检测这两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本对规定的质量指标值进行检测.表1是甲套设备的样本频数分布表,图1是乙套设备的样本频率分布直方图.

质量指标值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
频数 | 1 | 4 | 19 | 20 | 5 | 1 |
表1:甲套设备的样本频数分布表
(1)将频率视为概率,若乙套设备生产了5000件产品,则其中合格品约有多少件?
(2)填写下面2×2列联表,并根据列联表判断是否有95%的把握认为这种产品的质量指标值与甲乙两套设备的选择有关:
甲套设备 | 乙套设备 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
(3)根据表和图,对甲、乙两套设备的优劣进行比较.参考公式及数据:x2=![]()
P(Х2≥k) | 0.100 | 0.050 | 0.010 |
k | 2.706 | 3.841 | 6.635 |