题目内容
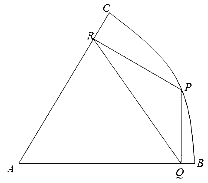
【题目】已知曲线![]() ,过点
,过点![]() 作直线
作直线![]() 和曲线
和曲线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求曲线![]() 的焦点到它的渐近线之间的距离;
的焦点到它的渐近线之间的距离;
(2)若![]() ,点
,点![]() 在第一象限,
在第一象限,![]() 轴,垂足为
轴,垂足为![]() ,连结
,连结![]() ,求直线
,求直线![]() 倾斜角的取值范围;
倾斜角的取值范围;
(3)过点![]() 作另一条直线
作另一条直线![]() ,
,![]() 和曲线
和曲线![]() 交于
交于![]() 、
、![]() 两点,问是否存在实数
两点,问是否存在实数![]() ,使得
,使得![]() 和
和![]() 同时成立?如果存在,求出满足条件的实数
同时成立?如果存在,求出满足条件的实数![]() 的取值集合,如果不存在,请说明理由.
的取值集合,如果不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]() (3)存在,实数
(3)存在,实数![]() 的取值集合为
的取值集合为![]()
【解析】
(1)求出曲线![]() 的焦点和渐近线方程,利用点到直线的距离公式求求解即可;
的焦点和渐近线方程,利用点到直线的距离公式求求解即可;
(2)设![]() ,
,![]() ,表示出直线
,表示出直线![]() 的斜率,根据
的斜率,根据![]() 的范围,求出其范围,进而得到倾斜角的取值范围;
的范围,求出其范围,进而得到倾斜角的取值范围;
(3)直接求出当直线![]() ,直线
,直线![]() 和当直线
和当直线![]() ,直线
,直线![]() 时,
时,![]() 的值,当
的值,当![]() 时,与双曲线联立可得
时,与双曲线联立可得![]() ,利用弦长公式求出
,利用弦长公式求出![]() 和
和![]() ,利用
,利用![]() 列方程求出
列方程求出![]() 的值,验证判别式成立即可得出结果.
的值,验证判别式成立即可得出结果.
(1)曲线![]() 的焦点为
的焦点为![]() ,渐近线方程
,渐近线方程![]() ,
,
由对称性,不妨计算![]() 到直线
到直线![]() 的距离,
的距离,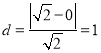 .
.
(2)设![]() ,
,![]() ,从而
,从而![]()
又因为点![]() 在第一象限,所以
在第一象限,所以![]() ,
,
从而![]() ,
,
所以直线![]() 倾斜角的取值范围是
倾斜角的取值范围是![]() ;
;
(3)当直线![]() ,直线
,直线![]()
![]() ,
,![]()
当直线![]() ,直线
,直线![]() 时,
时,![]()
不妨设![]() ,与双曲线联立可得
,与双曲线联立可得![]() ,
,
由弦长公式,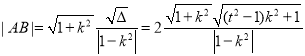
将![]() 替换成
替换成![]() ,可得
,可得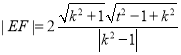
由![]() ,可得
,可得![]() ,
,
解得![]() ,此时
,此时![]() 成立.
成立.
因此满足条件的集合为![]()

练习册系列答案
相关题目