ЬтФПФкШн
ЁОЬтФПЁПШчЬтЫљЪО:ЩШаЮABCЪЧвЛПщАыОЖЮЊ2ЧЇУзЃЌдВаФНЧЮЊ60ЁуЕФЗчОАЧјЃЌPЕудкЛЁBCЩЯЃЌЯжгћдкЗчОАЧјжаЙцЛЎШ§ЬѕШ§ЬѕЩЬвЕНжЕРPQЁЂQRЁЂRPЃЌвЊЧѓНжЕРPQгыABДЙжБЃЌНжЕРPRгыACДЙжБЃЌжБЯпPQБэЪОЕкШ§ЬѕНжЕРЁЃ
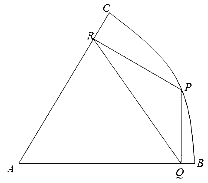
(1)ШчЙћPЮЛгкЛЁBCЕФжаЕуЃЌЧѓШ§ЬѕНжЕРЕФзмГЄЖШЃЛ
(2)гЩгкЛЗОГЕФдвђЃЌШ§ЬѕНжЕРPQЁЂPRЁЂQRУПФъФмВњЩњЕФОМУаЇвцЗжБ№ЮЊУПЧЇУз300ЭђдЊЁЂ200ЭђдЊМА400ЭђдЊЃЌЮЪ:етШ§ЬѕНжЕРУПФъФмВњЩњЕФОМУзмаЇвцзюИпЮЊЖрЩйЃП(ОЋШЗЕН1ЭђдЊ)
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ1222ЭђдЊ
ЃЛЃЈ2ЃЉ1222ЭђдЊ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩ![]() ЮЊгк
ЮЊгк![]() ЕФНЧЦНЗжЯпЩЯЃЌРћгУМИКЮЙиЯЕЃЌЗжБ№БэЪО
ЕФНЧЦНЗжЯпЩЯЃЌРћгУМИКЮЙиЯЕЃЌЗжБ№БэЪО![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌМДПЩ
ЃЌМДПЩ
ЧѓЕУШ§ЬѕНжЕРЕФзмГЄЖШЃЛЃЈ2ЃЉЩш![]() ЃЌ
ЃЌ![]() ЃЌИљОнШ§НЧКЏЪ§ЙиЯЕМАгрЯвЖЈРэЃЌМДПЩЧѓЕУ
ЃЌИљОнШ§НЧКЏЪ§ЙиЯЕМАгрЯвЖЈРэЃЌМДПЩЧѓЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌдђзмаЇвц
ЃЌдђзмаЇвц![]() ЃЌРћгУИЈжњНЧЙЋЪНМАе§ЯвКЏЪ§ЕФаджЪЃЌМДПЩЧѓЕУД№АИЃЎ
ЃЌРћгУИЈжњНЧЙЋЪНМАе§ЯвКЏЪ§ЕФаджЪЃЌМДПЩЧѓЕУД№АИЃЎ
ЃЈ1ЃЉгЩ![]() ЮЛгкЛЁ
ЮЛгкЛЁ![]() ЕФжаЕуЃЌдк
ЕФжаЕуЃЌдк![]() ЮЛгк
ЮЛгк![]() ЕФНЧЦНЗжЯпЩЯЃЌ
ЕФНЧЦНЗжЯпЩЯЃЌ
дђ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
гЩ![]() ЃЌЧв
ЃЌЧв![]() ЃЌ
ЃЌ
![]() ЮЊЕШБпШ§НЧаЮЃЌ
ЮЊЕШБпШ§НЧаЮЃЌ
дђ![]() ЃЌ
ЃЌ
Ш§ЬѕНжЕРЕФзмГЄЖШ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩш![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
дђ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]()
гЩгрЯвЖЈРэПЩжЊЃК![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
дђ![]() ЃЌ
ЃЌ
Ш§ЬѕНжЕРУПФъФмВњЩњЕФОМУзмаЇвц![]() ЃЌ
ЃЌ![]()
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ШЁзюДѓжЕЃЌзюДѓжЕЮЊ
ШЁзюДѓжЕЃЌзюДѓжЕЮЊ![]() ЃЌ
ЃЌ
Ш§ЬѕНжЕРУПФъФмВњЩњЕФОМУзмаЇвцзюИпдМЮЊ1222ЭђдЊЃЎ

 дФЖСПьГЕЯЕСаД№АИ
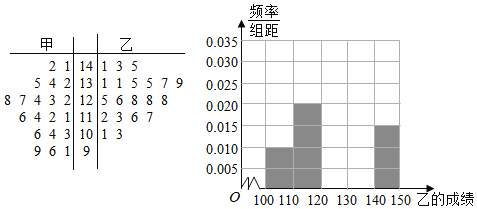
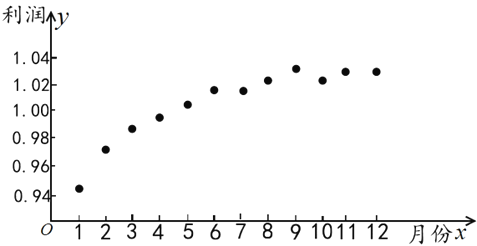
дФЖСПьГЕЯЕСаД№АИЁОЬтФПЁПШчЭМЪЧФГДДвЕЙЋЫО2017ФъУПдТЗнЙЋЫОРћШѓЃЈЕЅЮЛЃКАйЭђдЊЃЉЧщПіЕФЩЂЕуЭМЃКЮЊСЫдЄВтИУЙЋЫО2018ФъЕФРћШѓЧщПіЃЌИљОнЩЯЭМЪ§ОнЃЌНЈСЂСЫРћШѓyгыдТЗнxЕФСНИіЯпадЛиЙщФЃаЭЃКЂй![]() 0.94+0.028
0.94+0.028![]() ЃЛЂк
ЃЛЂк![]() 0.96+0.032lnxЃЌВЂЕУЕНвдЯТЭГМЦжЕЃК
0.96+0.032lnxЃЌВЂЕУЕНвдЯТЭГМЦжЕЃК
ФЃаЭЂй | ФЃаЭЂк | |
ВаВюЦНЗНКЭ | 0.000591 | 0.000164 |
змЦЋВюЦНЗНКЭ | 0.006050 | |
ЃЈ1ЃЉЧыРћгУЯрЙижИЪ§R2ХаЖЯФФИіФЃаЭЕФФтКЯаЇЙћИќКУЃЛ
ЃЈ2ЃЉЮЊСЫМЄРјдБЙЄЙЄзїЕФЛ§МЋадЃЌЙЋЫОУПдТЛсИљОнРћШѓЕФЧщПіНјааНБГЭЃЌМйЩшБОдТРћШѓЮЊy1ЃЌЖјЩЯвЛдТРћШѓЮЊy2ЃЌМЦЫуz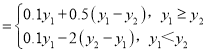 ЃЌВЂЙцЖЈЃКШєzЁн10ЃЌдђЯђШЋЬхдБЙЄЗЂЗХНБН№змЖюzдЊЃЛШєzЃМ10ЃЌДгШЋЬхдБЙЄУПШЫЕФЙЄзЪжаЕЙПл10ЉzдЊзїЮЊГЭЗЃЃЌПлЭъЮЊжЙЃЌЧыИљОнЃЈ1ЃЉжаФтКЯаЇЙћИќКУЕФЛиЙщФЃаЭЃЌЪддЄВт208Фъ4дТЗнИУЙЋЫОЕФНБГЭЧщПіЃПЃЈНсЙћОЋШЗЕНаЁЪ§ЕуКѓСНЮЛЃЉ
ЃЌВЂЙцЖЈЃКШєzЁн10ЃЌдђЯђШЋЬхдБЙЄЗЂЗХНБН№змЖюzдЊЃЛШєzЃМ10ЃЌДгШЋЬхдБЙЄУПШЫЕФЙЄзЪжаЕЙПл10ЉzдЊзїЮЊГЭЗЃЃЌПлЭъЮЊжЙЃЌЧыИљОнЃЈ1ЃЉжаФтКЯаЇЙћИќКУЕФЛиЙщФЃаЭЃЌЪддЄВт208Фъ4дТЗнИУЙЋЫОЕФНБГЭЧщПіЃПЃЈНсЙћОЋШЗЕНаЁЪ§ЕуКѓСНЮЛЃЉ
ВЮПМЪ§ОнМАЙЋЪНЃК![]() 1.73ЃЌ
1.73ЃЌ![]() 2.24ЃЌ1n2Ёж0.69ЃЌ1n3Ёж1.10ЃЌln5Ёж1.61ЃЎЯрЙижИЪ§R2ЃН1
2.24ЃЌ1n2Ёж0.69ЃЌ1n3Ёж1.10ЃЌln5Ёж1.61ЃЎЯрЙижИЪ§R2ЃН1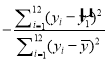 ЃЎ
ЃЎ