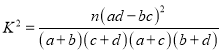题目内容
【题目】已知圆![]() 的半径为
的半径为![]() ,圆心在第一象限,且与直线
,圆心在第一象限,且与直线![]() 和
和![]() 轴都相切.
轴都相切.
(Ⅰ)求圆![]() 的方程.
的方程.
(Ⅱ)过![]() 的直线
的直线![]() 与圆相交所得的弦长为
与圆相交所得的弦长为![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() 或
或![]()
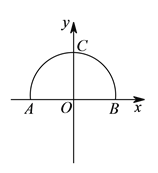
【解析】试题分析:(1)设圆标准方程,根据与![]() 轴相切得圆心坐标可设为
轴相切得圆心坐标可设为![]() ,再根据与直线
,再根据与直线![]() 相切得,圆心到直线距离等于半径2,解出参数a即得圆
相切得,圆心到直线距离等于半径2,解出参数a即得圆![]() 的方程.(2)先根据点斜式设直线方程,计算圆心到直线距离,再根据垂径定理列方程解出斜率,最后讨论斜率不存在时是否满足题意
的方程.(2)先根据点斜式设直线方程,计算圆心到直线距离,再根据垂径定理列方程解出斜率,最后讨论斜率不存在时是否满足题意
试题解析:(Ⅰ)∵ 圆与![]() 轴相切,且半径为
轴相切,且半径为![]() ,
,
∴圆心坐标可设为![]() ,
, ![]() ,
,
∵圆心到直线![]() 距离等于半径,
距离等于半径,
∴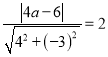 ,解得
,解得![]() ,
,
∴![]() 的方程为
的方程为![]() .
.
(Ⅱ)设![]() 直线方程为
直线方程为![]() ,即
,即![]() ,
,
易知圆心![]() 到
到![]() 的距离为
的距离为![]() ,
,
即: 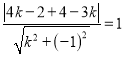 ,
,
解得![]() ,
, ![]() 的方程为:
的方程为: ![]() ;
;
当![]() 不存在时,
不存在时, ![]() 为
为![]() ,同样符合条件,
,同样符合条件,
综上所述![]() 的方程为
的方程为![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】某网站针对2015年中国好声音歌手A,B,C三人进行网上投票,结果如下
观众年龄 | 支持A | 支持B | 支持C |
20岁以下 | 100 | 200 | 600 |
20岁以上(含20岁) | 100 | 100 | 400 |
(1)在所有参与该活动的人中,用分层抽样的方法抽取n人,其中有6人支持A,求n的值.
(2)在支持C的人中,用分层抽样的方法抽取5人作为一个总体,从这5人中任意选取2人,求恰有1人在20岁以下的概率.