题目内容
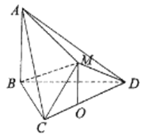
【题目】如图,在正四棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.
的中点.
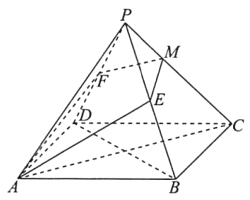
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(Ⅲ)若平面![]() 与棱
与棱![]() 交于点
交于点![]() ,求
,求![]() 的值.
的值.
【答案】(Ⅰ)见解析(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】试题分析:
(Ⅰ)设![]() ,则
,则![]() 为底面正方形
为底面正方形![]() 中心,连接
中心,连接![]() .因为
.因为![]() 为正四棱锥,所以
为正四棱锥,所以![]() 平面
平面![]() ,所以
,所以![]() .又
.又![]() ,根据线面垂直的判定定理即可证明结果.(Ⅱ)因为
,根据线面垂直的判定定理即可证明结果.(Ⅱ)因为![]() ,
, ![]() ,
, ![]() 两两互相垂直,如图建立空间直角坐标系
两两互相垂直,如图建立空间直角坐标系![]() ,然后再利用空间向量和法向量,即可求出结果;(Ⅲ)连接
,然后再利用空间向量和法向量,即可求出结果;(Ⅲ)连接![]() .设
.设![]() ,其中
,其中![]() ,则
,则![]() ,所以
,所以![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,又
,又![]() ,所以
,所以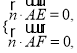 即
即![]() 可得
可得![]() ,因为
,因为![]() 平面
平面![]() ,所以
,所以![]() ,据此即可求出结果.
,据此即可求出结果.
试题解析:
(Ⅰ)设![]() ,则
,则![]() 为底面正方形
为底面正方形![]() 中心,连接
中心,连接![]() .
.
因为![]() 为正四棱锥,
为正四棱锥,
所以![]() 平面
平面![]() ,
,
所以![]() .
.
又![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)因为![]() ,
, ![]() ,
, ![]() 两两互相垂直,如图建立空间直角坐标系
两两互相垂直,如图建立空间直角坐标系![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
设![]() ,所以
,所以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
∴![]() ,
, ![]() .
.
∴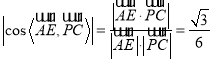 ,
,
即异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
(Ⅲ)连接![]() .
.
设![]() ,其中
,其中![]() ,则
,则![]() ,
,
所以![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,又
,又![]() ,所以
,所以 即
即![]()
所以![]() ,令
,令![]() ,
, ![]() ,所以
,所以![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
即![]() ,解得
,解得![]() ,所以
,所以![]() .
.


练习册系列答案
相关题目
【题目】某出租车公司响应国家节能减排的号召,已陆续购买了140辆纯电动汽车作为运营车辆,目前我国主流纯电动汽车按续航里程数![]() .(单位:公里)分为3类,即
.(单位:公里)分为3类,即![]() 类:
类:![]() ,
,![]() 类:
类:![]() ,
, ![]() 类:
类:![]() ,该公司对这140辆车的行驶总里程进行统计,结果如下表:
,该公司对这140辆车的行驶总里程进行统计,结果如下表:
类型 |
|
|
|
已行驶总里程不超过10万公里的车辆数 | 10 | 40 | 30 |
已行驶总里程超过10万公里的车辆数 | 20 | 20 | 20 |
(1)从这140辆汽车中任取一辆,求该车行驶总里程超过10万公里的概率;
(2)公司为了了解这些车的工作状况,决定抽取了14辆车进行车况分析,按表中描述的六种情况进行分层抽样,设从![]() 类车中抽取了
类车中抽取了![]() 辆车.
辆车.
①求![]() 的值;
的值;
②如果从这![]() 辆车中随机选取两辆车,求恰有一辆车行驶总里程超过10万公里的概率.
辆车中随机选取两辆车,求恰有一辆车行驶总里程超过10万公里的概率.