题目内容
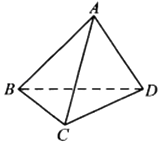
【题目】如图,三棱柱ABC﹣A1B1C1所有的棱长均为2,A1B= ![]() ,A1B⊥AC.
,A1B⊥AC. 
(Ⅰ)求证:A1C1⊥B1C;
(Ⅱ)求直线AC和平面ABB1A1所成角的余弦值.
【答案】证明:(Ⅰ)取AC中点O,连结A1O,BO,
∵三棱柱ABC﹣A1B1C1所有的棱长均为2,∴BO⊥AC,
∵A1B⊥AC,A1B∩BO=B,A1B面A1BO,BO面A1BO,
∴AC⊥面A1BO,
连结AB1,交A1B于点M,连结OM,则B1C∥OM,
又∵OM面A1BO,∴AC⊥OM,
∵A1C1∥AC,A1C1⊥B1C.
(Ⅱ)解:∵A1B⊥AB1,A1B⊥AC,∴A1B⊥面AB1C,
∴面AB1C⊥面ABB1A1,
∵面AB1C∩面ABB1A1=AB1,∴AC在平面ABB1A1的射影为AB1,
∴∠B1AC为直线AC和平面ABB1A1所成的角,
∵AB1=2AM=2 ![]() =
= ![]() ,
,
∴在 Rt△ACB1中,cos ![]() =
= ![]() =
= ![]() ,
,
∴直线AC和平面ABB1A1所成角的余弦值为 ![]() .
.
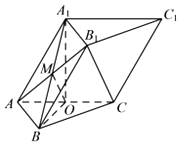
【解析】(Ⅰ)取AC中点O,连结A1O,BO,推导出BO⊥AC,A1B⊥AC,从而AC⊥面A1BO,连结AB1,交A1B于点M,连结OM,则B1C∥OM,从而AC⊥OM,由A1C1∥AC,能证明A1C1⊥B1C.(Ⅱ)由A1B⊥AB1,A1B⊥AC,得A1B⊥面AB1C,从而面AB1C⊥面ABB1A1,推导出AC在平面ABB1A1的射影为AB1,从而∠B1AC为直线AC和平面ABB1A1所成的角,由此能求出直线AC和平面ABB1A1所成角的余弦值.
【考点精析】利用直线与平面垂直的性质和空间角的异面直线所成的角对题目进行判断即可得到答案,需要熟知垂直于同一个平面的两条直线平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则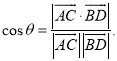 .
.

【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
频数 | 6 | 26 | 38 | 22 | 8 |

(1)作出这些数据的频数分布直方图;
(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中间值来代表这种产品质量的指标值);
(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的85%”的规定?