Question

【题目】在平面直角坐标系中．圆C的参数方程为 （α为参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，点D的极坐标为（ρ1 ， π）．
（1）求圆C的极坐标方程；
（2）过点D作圆C的切线，切点分别为A，B，且∠ADB=60°，求ρ1 ．

Answer 1

【答案】
（1）解：由 ，得 ，

两式平方相加得x2+（y﹣3）2=4．

即x2+y2﹣6y+5=0，

∴ρ2﹣6ρsinθ+5=0．

即圆C的极坐标方程为ρ2﹣6ρsinθ+5=0

（2）解：如图，D（ρ1，π）的直角坐标为（﹣ρ1，0），

|AC|=2，∠CAD=30°，则|CD|=4，

∴ ．

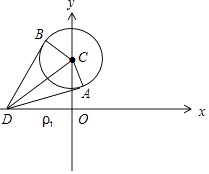
【解析】（1）利用平方关系消去参数θ，可得圆的直角坐标方程，结合公式ρ2=x2+y2，y=ρsinθ可得圆的极坐标方程；（2）画出图形，由D的极坐标得其直角坐标，数形结合得答案．