题目内容
【题目】已知数列{an}中,a2=2,其前n项和Sn满足: ![]() (n∈N*).
(n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
【答案】解:(Ⅰ)由题意有 ![]() .
.
所以 ![]() ,则有
,则有 ![]() (n≥2),
(n≥2),
所以2(Sn﹣Sn﹣1)=nan﹣(n﹣1)an﹣1,
即(n﹣2)an=(n﹣1)an﹣1(n≥2).
所以(n﹣1)an+1=nan,
两式相加得2(n﹣1)an=(n﹣1)(an+1+an﹣1),即2an=an+1+an﹣1(n≥2),
即an+1﹣an=an﹣an﹣1(n≥2,n∈N),
故数列{an}是等差数列.
又a1=0,a2=2,所以公差d=2,
所以数列{an}的通项公式为an=2n﹣2.
(Ⅱ)由(Ⅰ)知 ![]() ,
,
则 ![]() …+n22n﹣2,
…+n22n﹣2,
两边同乘以22得 ![]() +…+(n﹣1)22n﹣2+n22n,
+…+(n﹣1)22n﹣2+n22n,
两式相减得 ![]() +22n﹣2﹣n22n,
+22n﹣2﹣n22n,
即 ![]() =
= ![]() ,
,
所以 ![]()
【解析】(I)利用数列递推关系、等差数列的定义及其通项公式即可得出.(II)利用错位相减法、等比数列的求和公式即可得出.
【考点精析】利用数列的前n项和和数列的通项公式对题目进行判断即可得到答案,需要熟知数列{an}的前n项和sn与通项an的关系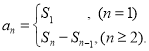 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
频数 | 6 | 26 | 38 | 22 | 8 |

(1)作出这些数据的频数分布直方图;
(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中间值来代表这种产品质量的指标值);
(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的85%”的规定?