题目内容
(本题满分10分)已知函数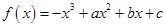 图象上的点
图象上的点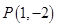 处的切线方程为
处的切线方程为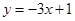 .(I)若函数
.(I)若函数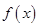 在
在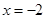 时有极值,求
时有极值,求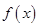 的表达式;
的表达式;
(Ⅱ)函数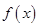 在区间
在区间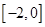 上单调递增,求实数
上单调递增,求实数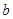 的取值范围.
的取值范围.
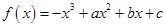 图象上的点
图象上的点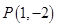 处的切线方程为
处的切线方程为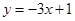 .(I)若函数
.(I)若函数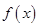 在
在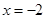 时有极值,求
时有极值,求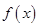 的表达式;
的表达式;(Ⅱ)函数
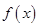 在区间
在区间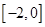 上单调递增,求实数
上单调递增,求实数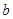 的取值范围.
的取值范围.(Ⅰ)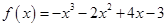 . (Ⅱ)实数
. (Ⅱ)实数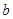 的取值范围为
的取值范围为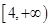 .
.
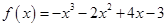 . (Ⅱ)实数
. (Ⅱ)实数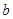 的取值范围为
的取值范围为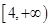 .
. 本试题主要是考查了运用导数的工具,来求解函数的极值和函数的单调性问题,以及导数几何意义的综合运用。
根据给定的曲线的切线方程得到切点坐标和极值点处导数为零得到相应的关系式进行分析得到解析式,再利用导数的符号判定单调性,进而得到范围。
解: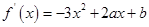 ,
,
因为函数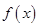 在
在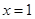 处的切线斜率为-3,
处的切线斜率为-3,
所以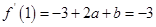 ,即
,即 , ①
, ①
又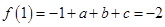 得
得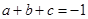 . ②
. ②
(Ⅰ)函数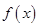 在
在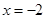 时有极值,
时有极值,
所以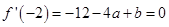 , ③
, ③
联立①②③解方程组,得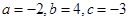 ,
,
所以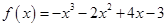 . ………………………6分
. ………………………6分
(Ⅱ)因为函数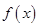 在区间
在区间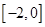 上单调递增,所以导函数
上单调递增,所以导函数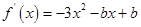 在区间
在区间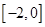 上的值恒大于或等于零,
上的值恒大于或等于零,
则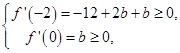
解得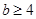 ,
,
所以实数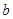 的取值范围为
的取值范围为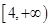 . ………………………10分
. ………………………10分
根据给定的曲线的切线方程得到切点坐标和极值点处导数为零得到相应的关系式进行分析得到解析式,再利用导数的符号判定单调性,进而得到范围。
解:
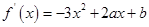 ,
, 因为函数
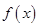 在
在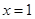 处的切线斜率为-3,
处的切线斜率为-3,所以
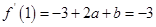 ,即
,即 , ①
, ①又
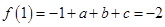 得
得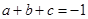 . ②
. ②(Ⅰ)函数
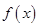 在
在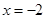 时有极值,
时有极值,所以
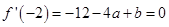 , ③
, ③ 联立①②③解方程组,得
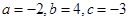 ,
, 所以
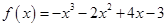 . ………………………6分
. ………………………6分(Ⅱ)因为函数
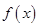 在区间
在区间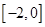 上单调递增,所以导函数
上单调递增,所以导函数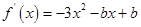 在区间
在区间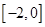 上的值恒大于或等于零,
上的值恒大于或等于零,则
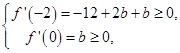
解得
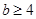 ,
, 所以实数
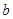 的取值范围为
的取值范围为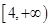 . ………………………10分
. ………………………10分
练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
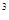 -x的切线的条数最多是( )
-x的切线的条数最多是( )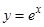 在点
在点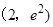 处的切线与两坐标轴所围成的三角形面积为( )
处的切线与两坐标轴所围成的三角形面积为( ) 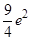
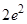
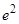
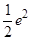
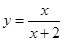 在点
在点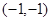 处的切线方程是
处的切线方程是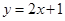
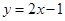
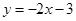
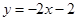
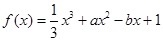 (
(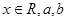 为实数)有极值,且在
为实数)有极值,且在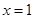 处的切线与直线
处的切线与直线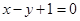 平行.
平行.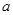 的取值范围;
的取值范围;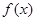 的极小值为1,若存在,求出实数
的极小值为1,若存在,求出实数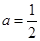 ,
,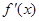 ,令
,令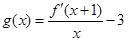
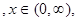
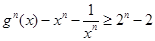
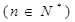
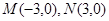 ,圆
,圆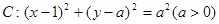 ,过
,过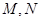 与圆
与圆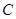 相切的两直线相交于点
相切的两直线相交于点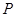 ,则点
,则点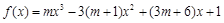 ,其中
,其中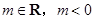 ,
,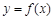 在(2,–3)处的切线方程;
在(2,–3)处的切线方程;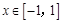 时,函数
时,函数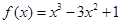 在
在 _____ 处取得极小值
_____ 处取得极小值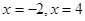 是函数
是函数 ,b=
,b=