题目内容
(本小题满分14分)
已知函数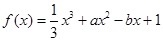 (
(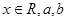 为实数)有极值,且在
为实数)有极值,且在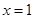 处的切线与直线
处的切线与直线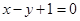 平行.
平行.
(1)求实数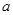 的取值范围;
的取值范围;
(2)是否存在实数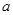 ,使得函数
,使得函数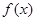 的极小值为1,若存在,求出实数
的极小值为1,若存在,求出实数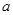 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)设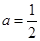 ,
,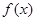 的导数为
的导数为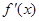 ,令
,令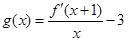
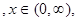
求证: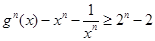
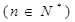
已知函数
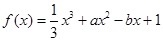 (
(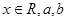 为实数)有极值,且在
为实数)有极值,且在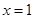 处的切线与直线
处的切线与直线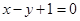 平行.
平行.(1)求实数
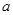 的取值范围;
的取值范围;(2)是否存在实数
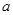 ,使得函数
,使得函数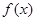 的极小值为1,若存在,求出实数
的极小值为1,若存在,求出实数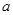 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;(3)设
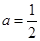 ,
,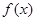 的导数为
的导数为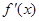 ,令
,令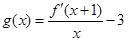
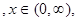
求证:
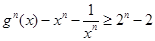
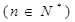
(1) 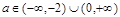 ;
;
(2)存在实数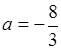 ,使得函数f(x)的极小值为1 ;
,使得函数f(x)的极小值为1 ;
(3)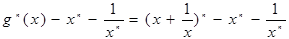
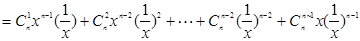
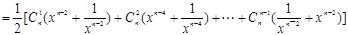
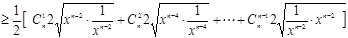
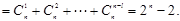
∴其中等号成立的条件为x=1,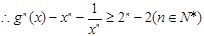
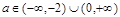 ;
;(2)存在实数
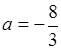 ,使得函数f(x)的极小值为1 ;
,使得函数f(x)的极小值为1 ;(3)
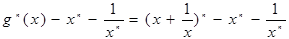
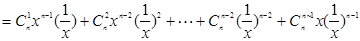
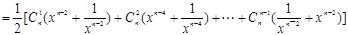
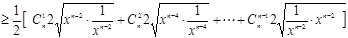
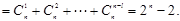
∴其中等号成立的条件为x=1,
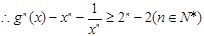
(1)根据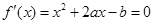 有两个不同的实数根,从而得到b,a的一个不等式,再根据
有两个不同的实数根,从而得到b,a的一个不等式,再根据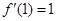 得到a,b的等式,消去b,可以解出a的取值范围.
得到a,b的等式,消去b,可以解出a的取值范围.
(2)直接求其极小值,根据极小值为1,求出a的值即可.
(3)先求出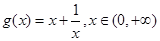 ,然后问题的关键是
,然后问题的关键是
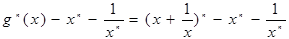
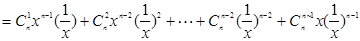
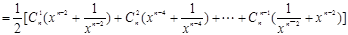
下面采用均值不等式进行证明即可.
解:(1)∵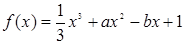 ,∴
,∴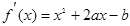 ,由题意∴f/(1)=1+2a-b=1,
,由题意∴f/(1)=1+2a-b=1,
∴b=2a. ① ……2分
∵f(x)有极值,∴方程f/(x)=x2+2ax-b=0有两个不等实根.
∴△=4a2+4b>0、 ∴a2+b>0. ②
由①、②可得,α2+2a>0.∴a<-2或a>0.故实数a的取值范围是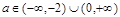 4分
4分
(2)存在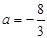 .……………5分
.……………5分
由(1)可知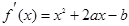 ,令f/(x)=0
,令f/(x)=0
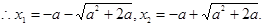

∴x=x2时,f(x)取极小值,则f(x2)=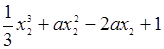 =1,
=1,
∴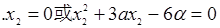 ……………………………………………………7分
……………………………………………………7分
若x2=0,即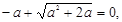 则a=0(舍).……………………8分
则a=0(舍).……………………8分
若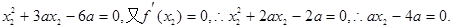
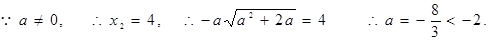
∴存在实数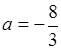 ,使得函数f(x)的极小值为1 ………9分
,使得函数f(x)的极小值为1 ………9分
(3)∵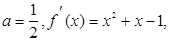
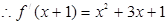 ,
,
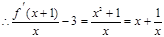
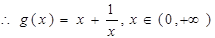 …….l0分
…….l0分
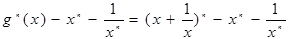
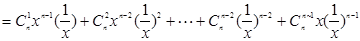
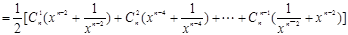
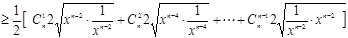
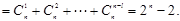
∴其中等号成立的条件为x=1…………………………………………………………13分
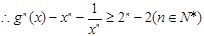 …………………………………………14分
…………………………………………14分
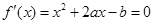 有两个不同的实数根,从而得到b,a的一个不等式,再根据
有两个不同的实数根,从而得到b,a的一个不等式,再根据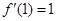 得到a,b的等式,消去b,可以解出a的取值范围.
得到a,b的等式,消去b,可以解出a的取值范围.(2)直接求其极小值,根据极小值为1,求出a的值即可.
(3)先求出
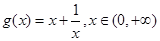 ,然后问题的关键是
,然后问题的关键是 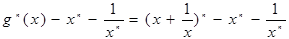
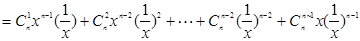
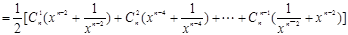
下面采用均值不等式进行证明即可.
解:(1)∵
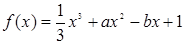 ,∴
,∴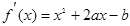 ,由题意∴f/(1)=1+2a-b=1,
,由题意∴f/(1)=1+2a-b=1,∴b=2a. ① ……2分
∵f(x)有极值,∴方程f/(x)=x2+2ax-b=0有两个不等实根.
∴△=4a2+4b>0、 ∴a2+b>0. ②
由①、②可得,α2+2a>0.∴a<-2或a>0.故实数a的取值范围是
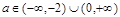 4分
4分(2)存在
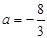 .……………5分
.……………5分由(1)可知
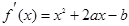 ,令f/(x)=0
,令f/(x)=0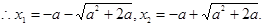

∴x=x2时,f(x)取极小值,则f(x2)=
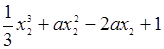 =1,
=1,∴
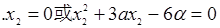 ……………………………………………………7分
……………………………………………………7分若x2=0,即
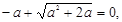 则a=0(舍).……………………8分
则a=0(舍).……………………8分若
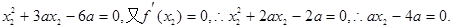
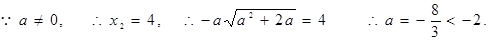
∴存在实数
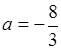 ,使得函数f(x)的极小值为1 ………9分
,使得函数f(x)的极小值为1 ………9分(3)∵
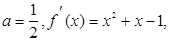
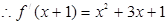 ,
, 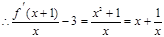
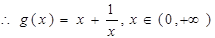 …….l0分
…….l0分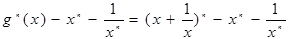
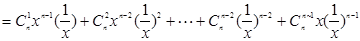
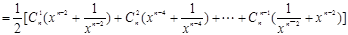
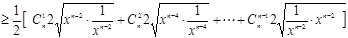
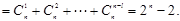
∴其中等号成立的条件为x=1…………………………………………………………13分
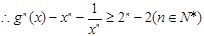 …………………………………………14分
…………………………………………14分
练习册系列答案
相关题目
 图象上的点
图象上的点 处的切线方程为
处的切线方程为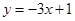 .(I)若函数
.(I)若函数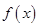 在
在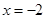 时有极值,求
时有极值,求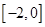 上单调递增,求实数
上单调递增,求实数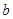 的取值范围.
的取值范围.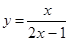 在点
在点 处的切线为l,则l上的点到
处的切线为l,则l上的点到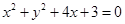 上的
上的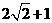

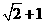
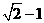
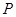 在曲线
在曲线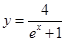 上,
上,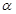 为曲线在点
为曲线在点 ,曲线
,曲线 在点(
在点( )处的
)处的
 的值;
的值;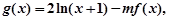 若当
若当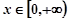 时,恒有
时,恒有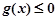 ,求
,求 的取值范围.
的取值范围.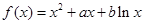 (
(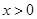 ,实数
,实数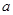 ,
,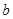 为常数).
为常数).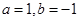 ,求
,求 在
在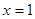 处的切线方程;
处的切线方程;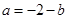 ,讨论函数
,讨论函数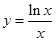 在点P(1,0)处的切线方程是 ( )
在点P(1,0)处的切线方程是 ( )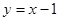
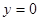

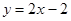
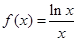 在点
在点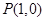 处的切线方程是 .
处的切线方程是 .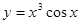 的导数是:( )
的导数是:( )


