题目内容
已知函数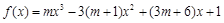 ,其中
,其中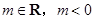 ,
,
(1)若m =" –" 2,求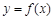 在(2,–3)处的切线方程;
在(2,–3)处的切线方程;
(2)当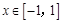 时,函数
时,函数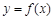 的图象上任意一点的切线斜率恒大于3 m,求m的取值范围.
的图象上任意一点的切线斜率恒大于3 m,求m的取值范围.
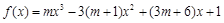 ,其中
,其中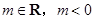 ,
,(1)若m =" –" 2,求
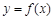 在(2,–3)处的切线方程;
在(2,–3)处的切线方程;(2)当
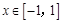 时,函数
时,函数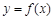 的图象上任意一点的切线斜率恒大于3 m,求m的取值范围.
的图象上任意一点的切线斜率恒大于3 m,求m的取值范围.解:(1)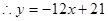 ;(2)
;(2) 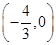 。
。
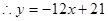 ;(2)
;(2) 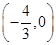 。
。本试题主要是考查了导数的几何意义的运用, 以及导数与不等式的综合运用。
(1),m =" –" 2,易知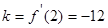 又过(2,-3)利用点斜式方程得到。
又过(2,-3)利用点斜式方程得到。
(2)要符合题意需要满足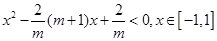 恒陈立,利用导数求解最值得到。
恒陈立,利用导数求解最值得到。
解:(1)易知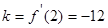 又过(2,-3)
又过(2,-3)
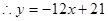 5分
5分
(2) 由已知得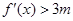 ,即
,即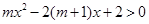 6分
6分
又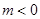 所以
所以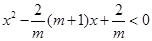 即
即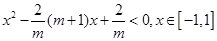 ①
①
设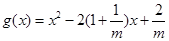 ,其函数开口向上,由题意知①式恒成立, 8分
,其函数开口向上,由题意知①式恒成立, 8分
所以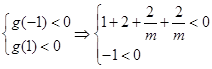 解之得
解之得
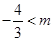 又
又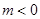 11分
11分
所以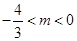
即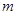 的取值范围为
的取值范围为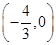 12分
12分
(1),m =" –" 2,易知
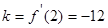 又过(2,-3)利用点斜式方程得到。
又过(2,-3)利用点斜式方程得到。(2)要符合题意需要满足
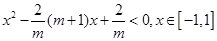 恒陈立,利用导数求解最值得到。
恒陈立,利用导数求解最值得到。解:(1)易知
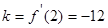 又过(2,-3)
又过(2,-3)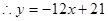 5分
5分(2) 由已知得
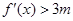 ,即
,即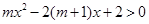 6分
6分又
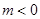 所以
所以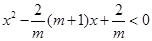 即
即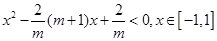 ①
①设
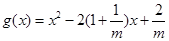 ,其函数开口向上,由题意知①式恒成立, 8分
,其函数开口向上,由题意知①式恒成立, 8分所以
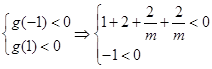 解之得
解之得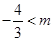 又
又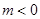 11分
11分所以
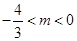
即
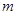 的取值范围为
的取值范围为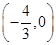 12分
12分
练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
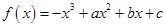 图象上的点
图象上的点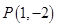 处的切线方程为
处的切线方程为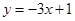 .(I)若函数
.(I)若函数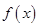 在
在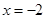 时有极值,求
时有极值,求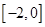 上单调递增,求实数
上单调递增,求实数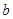 的取值范围.
的取值范围.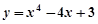 在区间
在区间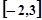 上的最小值为( )
上的最小值为( )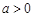 ,函数
,函数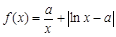 ,
,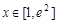 .
.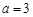 时,求曲线
时,求曲线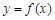 在点
在点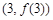 处的切线方程;
处的切线方程;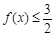 恒成立,求实数
恒成立,求实数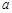 的取值范围.
的取值范围.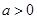 ,函数
,函数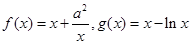 ,若对任意的
,若对任意的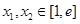 ,都有
,都有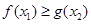 成立,则实数
成立,则实数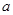 的取值范围为 .
的取值范围为 . 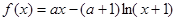
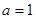 时,求
时,求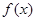 的单调区间;
的单调区间;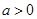 时,设
时,设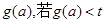 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.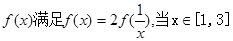 ,
,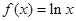 ,若在区间
,若在区间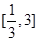 内,函数
内,函数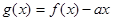 与 x轴有3个不同的交点,则实数a的取值范围是
与 x轴有3个不同的交点,则实数a的取值范围是 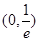
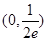
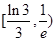
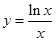 在点P(1,0)处的切线方程是 ( )
在点P(1,0)处的切线方程是 ( )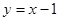
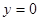

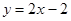
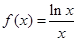 在点
在点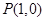 处的切线方程是 .
处的切线方程是 .