题目内容
已知函数f(x)=2x-2-x,数列{an}满足f(log2an)=-2n.
(1)求数列{an}的通项公式;
(2)求证:数列{an}是递减数列.
(1)求数列{an}的通项公式;
(2)求证:数列{an}是递减数列.
(1)an=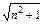 -n(2)证明见解析
-n(2)证明见解析
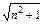 -n(2)证明见解析
-n(2)证明见解析(1)解 ∵f(x)=2x-2-x,
∴f(log2an)=2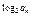 -2
-2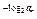 =-2n,
=-2n,
即an-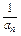 =-2n.∴a
=-2n.∴a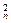 +2n·an-1=0.
+2n·an-1=0.
∴an=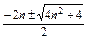 ,又an>0,∴an=
,又an>0,∴an=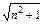 -n.
-n.
(2)证明 ∵an>0,且an=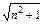 -n,
-n,
∴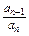 =
=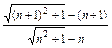 =
=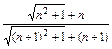 <1.
<1.
∴an+1<an.即{an}为递减数列.
∴f(log2an)=2
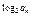 -2
-2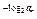 =-2n,
=-2n,即an-
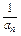 =-2n.∴a
=-2n.∴a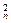 +2n·an-1=0.
+2n·an-1=0.∴an=
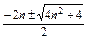 ,又an>0,∴an=
,又an>0,∴an=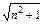 -n.
-n.(2)证明 ∵an>0,且an=
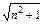 -n,
-n,∴
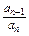 =
=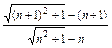 =
=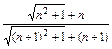 <1.
<1.∴an+1<an.即{an}为递减数列.

练习册系列答案
相关题目
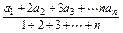 ,若{bn}为等差数列,求证:{an}也为等差数列.
,若{bn}为等差数列,求证:{an}也为等差数列.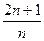
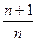
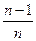
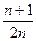
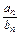 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.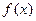 满足下列条件:
满足下列条件: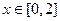 ,总有
,总有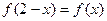 ,且
,且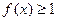 ,
,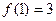 ;
;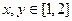 ,若
,若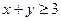 ,则
,则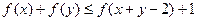 .
.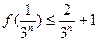 (
(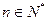 );(2)
);(2)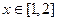 时,
时,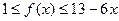 .
.