Question

【题目】已知椭圆经过点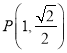，且两焦点与短轴的一个端点的连线构成等腰直角三角形．

（）求椭圆的方程．

（）过定点的动直线，交椭圆于、两点，试问：在坐标平面上是否存在一个定点，使得以为直径的圆恒过点．若存在，求出点的坐标；若不存在，请说明理由．

Answer 1

【答案】(1) ；(2)答案见解析.

【解析】试题分析：（）由题可知，则，椭圆经过点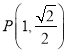，带入可得，由此可知所求椭圆方程为；(2)分别求出与轴平行时和与轴垂直时得圆得方程，联立可求得两圆得切点，进而推断所求的点如果存在只能是，当直线与轴垂直时，以为直径的圆过点，当直线不垂直于轴时设直线的方程为，与椭圆的方程联立求得，证明出,即以为直径得圆恒过点.

试题解析：（）∵椭圆的两焦点与短轴的一个端点的连线构成等腰直角三角形，

∴，

∴，

又∵椭圆经过点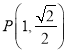，代入可得，

∴，故所求椭圆方程为．

（）当与轴平行时，以为直径的圆的方程： ，

当与轴垂直时，以为直径的圆的方程： ，

由，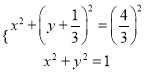

解得，

即两圆公共点，因此，所求的点如果存在，只能是．

（i）当直线斜率不存在时，以为直径的圆过点．

（ii）若直线斜率存在时，可设直线．

由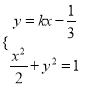，消去得： ，

记点、，

则，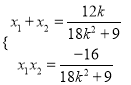

∵， ，

∴，

．

∴，

综合（i）（ii），以为直径的圆恒过点．