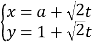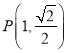题目内容
【题目】如图,已知三棱柱![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.

(1)证明:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由题意首先证得线面垂直,然后利用线面垂直的定义即可证得线线垂直;
(2)建立空间直角坐标系,分别求得直线的方向向量和平面的法向量,然后结合线面角的正弦值和同角三角函数基本关系可得线面角的余弦值.
(1)如图所示,连结![]() ,
,
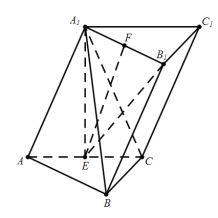
等边![]() 中,
中,![]() ,则
,则![]() ,
,
平面ABC⊥平面![]() ,且平面ABC∩平面
,且平面ABC∩平面![]() ,
,
由面面垂直的性质定理可得:![]() 平面
平面![]() ,故
,故![]() ,
,
由三棱柱的性质可知![]() ,而
,而![]() ,故
,故![]() ,且
,且![]() ,
,
由线面垂直的判定定理可得:![]() 平面
平面![]() ,
,
结合![]() 平面
平面![]() ,故
,故![]() .
.
(2)在底面ABC内作EH⊥AC,以点E为坐标原点,EH,EC,![]() 方向分别为x,y,z轴正方向建立空间直角坐标系
方向分别为x,y,z轴正方向建立空间直角坐标系![]() .
.
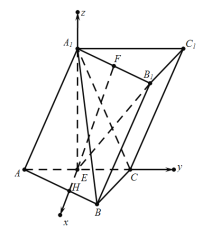
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
据此可得: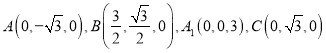 ,
,
由![]() 可得点
可得点![]() 的坐标为
的坐标为![]() ,
,
利用中点坐标公式可得:![]() ,由于
,由于![]() ,
,
故直线EF的方向向量为:![]()
设平面![]() 的法向量为
的法向量为![]() ,则:
,则:
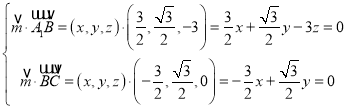 ,
,
据此可得平面![]() 的一个法向量为
的一个法向量为![]() ,
,![]()
此时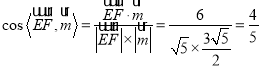 ,
,
设直线EF与平面![]() 所成角为
所成角为![]() ,则
,则![]() .
.

【题目】已知函数f(x)=|x﹣a|+2a,且不等式f(x)≤4的解集为{x|﹣1≤x≤3}.
(1)求实数a的值.
(2)若存在实数x0,使f(x0)≤5m2+m﹣f(﹣x0)成立,求实数m的取值范围.
【题目】为了研究经常使用手机是否对数学学习成绩有影响,某校高二数学研究性学习小组进行了调查,随机抽取高二年级50名学生的一次数学单元测试成绩,并制成下面的2×2列联表:
及格 | 不及格 | 合计 | |
很少使用手机 | 20 | 5 | 25 |
经常使用手机 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
则有( )的把握认为经常使用手机对数学学习成绩有影响.
参考公式: ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A.97.5%B.99%C.99.5%D.99.9%