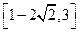题目内容
(本小题满分14分)已知动圆与直线 相切,且过定点F(1, 0),动圆圆心为M.
相切,且过定点F(1, 0),动圆圆心为M.
(1)求点M的轨迹C的方程;
(2)若直线l与曲线C交于A、B两点,且 (O为坐标原点),求证:直线l过一定点.
(O为坐标原点),求证:直线l过一定点.
 相切,且过定点F(1, 0),动圆圆心为M.
相切,且过定点F(1, 0),动圆圆心为M.(1)求点M的轨迹C的方程;
(2)若直线l与曲线C交于A、B两点,且
 (O为坐标原点),求证:直线l过一定点.
(O为坐标原点),求证:直线l过一定点. ,直线AB过定点 (5, 0).
,直线AB过定点 (5, 0).解:(1)由已知,点M到直线 的距离等于到点(1,0)的距离,所以点M是以F(1, 0)为焦点,以
的距离等于到点(1,0)的距离,所以点M是以F(1, 0)为焦点,以 为准线的抛物线,焦点到准线的距离p = 2, ........2分
为准线的抛物线,焦点到准线的距离p = 2, ........2分
∴ 点M的轨迹方程为 . .........4分
. .........4分
(2)设 ,由
,由 可得:
可得: ①
①
∵ A、B均在抛物线上,
∴ Þ
Þ ②
②
由①②可得: ,
,
∴ 或
或 (舍去). .............8分
(舍去). .............8分
再由 相减得:
相减得: ,
,
若 ,则AB⊥x轴,
,则AB⊥x轴, ,由①:
,由①: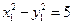 ,结合
,结合 得:
得: ,
,
∴ 此时AB的方程为 . ..............9分
. ..............9分
若 ,则
,则 ,即为直线AB的斜率,而
,即为直线AB的斜率,而 ,则AB的方程为:
,则AB的方程为:
 , .............11分
, .............11分
即 ,
,
∴ 也过定点 (5, 0). ...............13分
也过定点 (5, 0). ...............13分
综上得,直线AB过定点 (5, 0). ...............14分
 的距离等于到点(1,0)的距离,所以点M是以F(1, 0)为焦点,以
的距离等于到点(1,0)的距离,所以点M是以F(1, 0)为焦点,以 为准线的抛物线,焦点到准线的距离p = 2, ........2分
为准线的抛物线,焦点到准线的距离p = 2, ........2分∴ 点M的轨迹方程为
 . .........4分
. .........4分(2)设
 ,由
,由 可得:
可得: ①
① ∵ A、B均在抛物线上,
∴
 Þ
Þ ②
② 由①②可得:
 ,
,∴
 或
或 (舍去). .............8分
(舍去). .............8分再由
 相减得:
相减得: ,
,若
 ,则AB⊥x轴,
,则AB⊥x轴, ,由①:
,由①: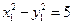 ,结合
,结合 得:
得: ,
,∴ 此时AB的方程为
 . ..............9分
. ..............9分若
 ,则
,则 ,即为直线AB的斜率,而
,即为直线AB的斜率,而 ,则AB的方程为:
,则AB的方程为: , .............11分
, .............11分即
 ,
,∴
 也过定点 (5, 0). ...............13分
也过定点 (5, 0). ...............13分综上得,直线AB过定点 (5, 0). ...............14分

练习册系列答案
相关题目
 上移动,等腰△OPA的顶角∠OPA为120°(O,P,A按顺时针方向排列),求点P的轨迹方程
上移动,等腰△OPA的顶角∠OPA为120°(O,P,A按顺时针方向排列),求点P的轨迹方程
 ,若点P满足
,若点P满足 。
。 与点P的轨迹交于A、B两点,若
与点P的轨迹交于A、B两点,若 ,且曲线E上存在点C,使
,且曲线E上存在点C,使 ,求实数
,求实数
 ,若按向量
,若按向量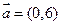 作平移变换得曲线
作平移变换得曲线 ;若将曲线
;若将曲线 按伸缩系数
按伸缩系数 向着
向着 轴作伸缩变换,再按伸缩系数3向着
轴作伸缩变换,再按伸缩系数3向着 轴作伸缩变换得到曲线
轴作伸缩变换得到曲线
 为
为 为
为 与曲线
与曲线 上的动点,点Q在NP上,点G在MP上,且满足
上的动点,点Q在NP上,点G在MP上,且满足 .
. 是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.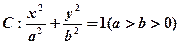 的离心率为
的离心率为 ,且过点
,且过点 。
。 的方程;
的方程; 与椭圆
与椭圆 ,
, ,求
,求 的值。
的值。 是过圆锥曲线中心的任一条弦,
是过圆锥曲线中心的任一条弦, 是二次曲线上异于
是二次曲线上异于 的任一点,且
的任一点,且 均与坐标轴不平行,则对于椭圆
均与坐标轴不平行,则对于椭圆 ,有
,有 ,类似的,对于双曲线
,类似的,对于双曲线 ,有
,有 。
。 ,试在此区间内确定t的值,使图中的阴影部分面积s1与s2之和最小.
,试在此区间内确定t的值,使图中的阴影部分面积s1与s2之和最小.

 有公共点,则b的取值范围是
有公共点,则b的取值范围是