题目内容
(本小题满分13分)已知函数f(x)=-x2+2ax+1-a在x∈[0,1]时有最大值2,求a的值.
a=2,或a=-1.
试题分析:二次函数求最值,要注意讨论对称轴与区间的位置关系,求出最值后等于2,即可求a的值
f(x)=-(x-a)2+a2-a+1,
当a≥1时,ymax=a;
当0<a<1时,ymax=a2-a+1;
当a≤0时,ymax=1-a.
根据已知条件:
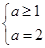
或
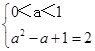 或
或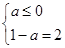
解得a=2,或a=-1.
点评:二次函数最值问题,注意对称轴与区间的位置关系,当对称轴于区间的位置关系不确定时,须分类讨论,从而得到原函数的单调性,进而可以求最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 对任意实数
对任意实数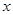 都满足
都满足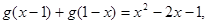 且
且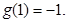
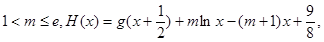 求证:
求证: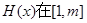 上为减函数;
上为减函数;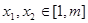 ,恒有
,恒有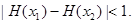
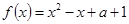
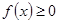 对一切实数
对一切实数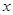 恒成立,求实数
恒成立,求实数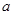 的取值范围.
的取值范围.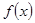 在区间
在区间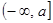 上的最小值
上的最小值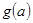 的表达式.
的表达式.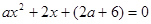 至少有一个负实数根的充要条件是a
至少有一个负实数根的充要条件是a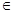 _______
_______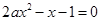 在(0,1)内恰有一解,则
在(0,1)内恰有一解,则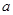 的取值范围是
的取值范围是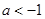
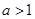
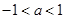
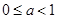
 的单调增区间为 ;
的单调增区间为 ;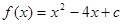 ,求
,求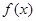 的单调递减区间。
的单调递减区间。 在区间
在区间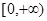 上单调递减,求实数
上单调递减,求实数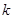 的取值范围。
的取值范围。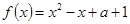
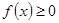 对一切实数x恒成立,求实数a的取值范围。
对一切实数x恒成立,求实数a的取值范围。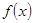 在区间
在区间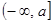 上的最小值
上的最小值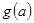 的表达式。
的表达式。 满足
满足 ;
; 有唯一解,求
有唯一解,求 的值;
的值; 在区间
在区间 上不是单调函数,求实数
上不是单调函数,求实数 的取值范围.
的取值范围.