题目内容
【题目】已知数列{![]() }的前n项和
}的前n项和![]() (n为正整数)。
(n为正整数)。
(1)令![]() ,求证数列{
,求证数列{![]() }是等差数列,并求数列{
}是等差数列,并求数列{![]() }的通项公式;
}的通项公式;
(2)令![]() ,
,![]() 试比较
试比较![]() 与
与![]() 的大小,并予以证明.
的大小,并予以证明.
【答案】(1)![]() (2)当
(2)当![]()
![]() ,当
,当![]() 时
时![]() .
.
【解析】
试题分析:(1)已知![]() ,一般利用
,一般利用![]() 进行化简条件,当
进行化简条件,当![]() 时,
时,![]() ,
,![]() ,又
,又![]() 数列
数列![]() 是首项和公差均为1的等差数列,于是
是首项和公差均为1的等差数列,于是![]() .(2)由(1)得
.(2)由(1)得![]() ,是等差乘等比型,所以其和求法为“错位相减法”, 即得
,是等差乘等比型,所以其和求法为“错位相减法”, 即得![]() .数列中比较大小,一般用作差,即
.数列中比较大小,一般用作差,即![]() ,而比较
,而比较![]() 的大小,有两个思路,一是数学归纳法,二是二项展开式定理.
的大小,有两个思路,一是数学归纳法,二是二项展开式定理.
试题解析:(1)在![]() 中,令n=1,可得
中,令n=1,可得![]() ,即
,即![]() 1
1
当![]() 时,
时,![]() , 2
, 2
![]() .
.
![]()
又![]() 数列
数列
于是![]() .6
.6
(2)由(1)得![]() ,所以
,所以
![]()
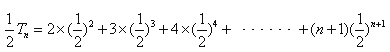
由①-②得![]()
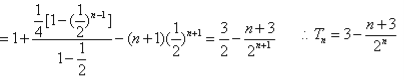 9
9
![]() 2
2
于是确定![]() 的大小关系等价于比较
的大小关系等价于比较![]() 的大小
的大小
![]()
猜想:当![]() 证明如下:
证明如下:
证法1:(1)当n=3时,由猜想显然成立.
(2)假设![]() 时猜想成立.即
时猜想成立.即![]()
则![]() 时,
时,![]()
所以当![]() 时猜想也成立
时猜想也成立
综合(1)(2)可知 ,对一切![]() 的正整数,都有
的正整数,都有![]()
证法2:当![]() 时
时
![]()
综上所述,当![]()
![]() ,当
,当![]() 时
时![]() 14
14

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目