题目内容
已知数列{an}的前n项和为Sn,且Sn=2an-1;数列{bn}满足bn-1-bn=bnbn-1(n≥2,n∈N*),b1=1.
(1)求数列{an},{bn}的通项公式;
(2)求数列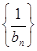 的前n项和Tn.
的前n项和Tn.
(1)求数列{an},{bn}的通项公式;
(2)求数列
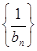 的前n项和Tn.
的前n项和Tn.(1)an=2n-1,bn=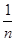 (2)(n-1)·2n+1.
(2)(n-1)·2n+1.
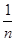 (2)(n-1)·2n+1.
(2)(n-1)·2n+1.(1)由Sn=2an-1,得S1=2a1-1,∴a1=1.
又Sn=2an-1,Sn-1=2an-1-1(n≥2),
两式相减,得Sn-Sn-1=2an-2an-1,an=2an-2an-1.
∴an=2an-1,n≥2.∴数列{an}是首项为1,公比为2的等比数列.
∴an=1·2n-1=2n-1.
由bn-1-bn=bnbn-1(n≥2,n∈N*),得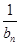 -
-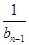 =1.
=1.
又b1=1,∴数列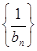 是首项为1,公差为1的等差数列.
是首项为1,公差为1的等差数列.
∴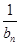 =1+(n-1)·1=n.∴bn=
=1+(n-1)·1=n.∴bn=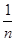 .
.
(2)由(1)可知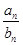 =n·2n-1,
=n·2n-1,
∵Tn=1·20+2·21+…+n·2n-1,∴2Tn=1·21+2·22+…+n·2n.
两式相减,得-Tn=1+21+…+2n-1-n·2n=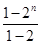 -n·2n=-1+2n-n·2n.
-n·2n=-1+2n-n·2n.
∴Tn=(n-1)·2n+1
又Sn=2an-1,Sn-1=2an-1-1(n≥2),
两式相减,得Sn-Sn-1=2an-2an-1,an=2an-2an-1.
∴an=2an-1,n≥2.∴数列{an}是首项为1,公比为2的等比数列.
∴an=1·2n-1=2n-1.
由bn-1-bn=bnbn-1(n≥2,n∈N*),得
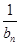 -
-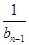 =1.
=1.又b1=1,∴数列
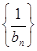 是首项为1,公差为1的等差数列.
是首项为1,公差为1的等差数列.∴
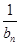 =1+(n-1)·1=n.∴bn=
=1+(n-1)·1=n.∴bn=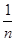 .
.(2)由(1)可知
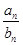 =n·2n-1,
=n·2n-1,∵Tn=1·20+2·21+…+n·2n-1,∴2Tn=1·21+2·22+…+n·2n.
两式相减,得-Tn=1+21+…+2n-1-n·2n=
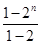 -n·2n=-1+2n-n·2n.
-n·2n=-1+2n-n·2n.∴Tn=(n-1)·2n+1

练习册系列答案
相关题目
 和
和 中,已知
中,已知 .
. ,求数列
,求数列 的前n项和
的前n项和 .
. ,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=2,点(an,an+1)在函数f(x)=2x2+2x的图象上,其中n为正整数.
,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=2,点(an,an+1)在函数f(x)=2x2+2x的图象上,其中n为正整数. =an,则a3= ;{an}的前n项和Sn= .
=an,则a3= ;{an}的前n项和Sn= .  an+
an+ ,则{an}的通项公式是an=________.
,则{an}的通项公式是an=________. 的等比数列{an}的前n项和为Sn,则( )
的等比数列{an}的前n项和为Sn,则( )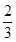 的等比数列{an}的前n项和为Sn,则 ( ).
的等比数列{an}的前n项和为Sn,则 ( ).