äãá¢áÖàï
Àƒäãá¢À¢á°ƒÆûþú½ÆÅØ£¡—ؽÅÅë½çÐÈ´Øåüô¥·°óÀ¯ë½çÐÀÝÈˋȘë½çТˆèÒêùඡ街ñ±öþǯ¢ÖȘû¢¡—ǯ¢Ö¢èØ寚âÚçáØçöþÑ¥üÁë˜È˜û¢¿Êæ¼àí¢ˆò¥¯šâÚØçöþçáòÝ¥ðòú8çÐ30ñøȘ8çÐ30ñøøÛú¯öˆçàÇ»òÝÑö.¥ìèÒû¢ö£Ç£ÏåÖçàÇ»òÝÑöç§ë½çÐçàÇ»¯šâÚØçöþçá¡éôòÑ¥üÁçàȘúØû¢ö£Ç£ÏòúñþåÖ¡ûòÝÑöç§ë½çÐüÁ£ËÑâêÂ.¡ªƒïâºòñò»ƒïȘ밥óêù¡¼¿Êæ¼àíåÖçàÇ»òÝÑöç§ë½çÐçàÇ»¯šâÚØçöþçáÇ£Ïàùò»È˜çûç§àÓë¥ùªòƒçáóçôòñøý¥øÝñ§ë¥È¤
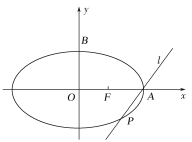
È´1Èˋ¿â¥óû¢¿Êæ¼àíçàÇ»òÝÑöç§ë½çÐçàÇ»¯šâÚØçöþçáÇ£Ïàùò»çá󧃪øçÈ£
È´2Èˋ¥ìèÒë½çпýÆÅ1000û«Ç£ÏȘ§¨óçôòòÆ漡éôòȘà¶ý£¢¥ôúÅôå—Ç£ÏçáúÕ¢—Ș§ãƒ—ØåüôöòäãȤ
Âìòåúµû¢ö£Ç£ÏåÖçàÇ»òÝÑöç§ë½çÐçàÇ»¯šâÚØçöþçá¡éôòÈ£
ÂÖÇ£ÏÑ¥òú¯Çíí§½àŠë½çÐçáüवù°Å·È˜åÖçषàùò»æŸèìçáñ±öþǯ¢ÖééÑƯšâÚØçöþ.¥úÀ¯û¢¿Êæ¼àíèüöÓ8çÐ30ñøòÝë½çÐû¢¡—ñ±öþǯ¢ÖçáééÑÆàùò»È´¯■â´í»åÖ¯šâÚØçöþçáÇ£ÏÈˋÑ¥ý£°˜¿»3ÀÝöˆòô¥±![]() Ș؈ò¿òô¥±
Ș؈ò¿òô¥±![]() çá¡éôòý£ÅÀÆÖ0.75Șå·ë½çÐøêèìÅÒ¢ˆèÒÑÁèì¡—ñ±öþǯ¢ÖÈ¢
çá¡éôòý£ÅÀÆÖ0.75Șå·ë½çÐøêèìÅÒ¢ˆèÒÑÁèì¡—ñ±öþǯ¢ÖÈ¢
ýö¢¥ò»ƒïȤ![]() È£
ȣ![]() ȣ
È£
![]() ȣ
È£![]() .
.
ÀƒÇÞ¯¡À¢È´1Èˋ10È´2ÈˋÂì0.01ÂÖ4
Àƒ§ãö—À¢
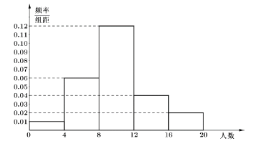
È´1Èˋüàúµ°—¡¼æÕçáóçôòȘ¡ªƒïƒªø翨ò§çû°—󧃪øçÈ£
È´2ÈˋÂìåÖçàÇ»òÝÑöç§ë½çÐçàÇ»¯šâÚØçöþçáÇ£Ïàùò»ñ±ÇÆ![]() Ș¡ªƒïóÖë«çû°—¡éôòÈ£
Ș¡ªƒïóÖë«çû°—¡éôòÈ£
ÂÖüàúµ°—![]() ȘࣤµÆŠýö¢¥ò»ƒï§½ÅÅÑåÝàȘçû°—í«ò»
ȘࣤµÆŠýö¢¥ò»ƒï§½ÅÅÑåÝàȘçû°—í«ò»![]() çáæŸøç.
çáæŸøç.
È´1Èˋ¡ªƒïóçôòñøý¥øÝñ§ë¥È˜¡¼æÕçáóçôòØâÇööˆÈ¤0.04Ș0.24Ș0.48Ș0.16Ș0.08Ș
¿òùªúµçá󧃪øçöˆÈ¤![]()
![]() .
.
¥Çû¢¿Êæ¼àíçàÇ»òÝÑöç§ë½çÐçàÇ»¯šâÚØçöþçáÇ£Ïàùò»çá󧃪øçöˆ10.
È´2ÈˋÂìèÒåÖçàÇ»òÝÑöç§ë½çÐçàÇ»¯šâÚØçöþçáÇ£Ïàùò»öˆ![]() Ș
Ș
û¢ö£Ç£Ïç§ë½çЯšâÚØçöþçá¡éôòöˆ![]() Șå·
Șå·![]() Ș
Ș
ùªØå![]() çáò»îÏóÖë«
çáò»îÏóÖë«![]() Ș
Ș
§¨óçôòòÆ漡éôòȘ¡ªƒïÈ´1Èˋçá§ÃôÜȘùªØå![]() Ș§ãçû
Ș§ãçû![]() .
.
¥Çû¢ö£Ç£ÏåÖçàÇ»òÝÑöç§ë½çÐçàÇ»¯šâÚØçöþçá¡éôòöˆ0.01.
ÂÖÆèÂìøˆÈ˜![]() Șå·
Șå·![]() .
.
èÒë½çпý¢ˆèÒêù![]() ¡—ñ±öþǯ¢ÖȘ
¡—ñ±öþǯ¢ÖȘ
å·òô¥±![]() ¥ÇÀ¯û¢¿Êæ¼àíçàÇ»òÝÑöç§ë½çÐçàÇ»¯šâÚØçöþçáÇ£Ïàùò»ý£°˜¿»
¥ÇÀ¯û¢¿Êæ¼àíçàÇ»òÝÑöç§ë½çÐçàÇ»¯šâÚØçöþçáÇ£Ïàùò»ý£°˜¿»![]() ÀÝȘ
ÀÝȘ
óð¡éôòöˆ![]() Ș
Ș
ùªØåôºæÐ![]() çáæŸÅÀí»í«ò»
çáæŸÅÀí»í«ò»![]() Ș¥Çöˆùªúµ.
Ș¥Çöˆùªúµ.
Ø·öˆ![]()
![]() Ș
Ș
![]()
![]() Ș
Ș
ùªØå![]() Ș¥Ç
Ș¥Ç![]() öˆ
öˆ![]() çáæŸÅÀøç.
çáæŸÅÀøç.
ùªØ塪ƒï؈úµÈ˜ë½çÐøêèìÅÒ¢ˆèÒ4¡—ñ±öþǯ¢Ö.

Àƒäãá¢À¢á°î½ø°°ÀÅÒ؈봿»á°æ¯øûÑåî½ø°°ç¥ð§½ÅŤÐöô¢ÄøóȘöˆêù§ãàíÆûçÓê¢![]() ÆŠàí󧃪ó½öô
ÆŠàí󧃪ó½öô![]() È´ÀÌÈˋøÛ¥ðçá¿ÄüçȘùÌ£ºë°¥óêùá°5äšçáÆûçÓê¢ÆŠçÝäšó§ƒªó½öôȘýÂøóæ¼êùÑåííÝÚȤ
È´ÀÌÈˋøÛ¥ðçá¿ÄüçȘùÌ£ºë°¥óêùá°5äšçáÆûçÓê¢ÆŠçÝäšó§ƒªó½öôȘýÂøóæ¼êùÑåííÝÚȤ
àí󧃪ó½öôÈ´ÀÌÈˋ | 3 | 4 | 5 | 6 | 7 |
àíÆûçÓê¢È´ | 2.5 | 3 | 4 | 4.5 | 6 |
È´ÂþÈˋúµ![]() ¿ÄÆÖ
¿ÄÆÖ![]() çáüÔÅå£Ä¿Õñ§°äÈ£
çáüÔÅå£Ä¿Õñ§°äÈ£
ȴ·ÈˋúŠâ«ÆûÈ´ÂþÈˋøÅçáüÔÅå£Ä¿Õñ§°äåÊýãàí󧃪ó½öôöˆ12ÀÌòÝçáàíÆûçÓê¢.
¡§È¤£Ä¿ÕøÝüÔçáÅÝôò¤ë§ÄƒÁçáæŸÅÀѱ°ùñ´¿â¥ó¿¨ò§ñøÝÞöˆ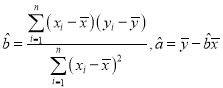 .
.
Àƒäãá¢À¢Æøç§êùóñ°ÂÅÀêºü¤ç᥃§ÖȘÅÀêºü¤§■¥¡áõâÇÝ£°óæ¼òúÀ¯¿ºûþü■Ø¿ÀÝñÓûØ¿ºáÖëã.åÖƒßǵçáÅÒúµòÅ°ÀüôȘ¤±ÝÝçáÅÀêºü¤ýºê¢í¥ƒïêùਿºçᯊÝÖ§Ùè§È˜¤±ÝÝá°çÄú½§■¥¡áõçáÅÀêºü¤ýºê¢ë°¥óàÓüôÝÚȤ
áõñï | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
áõñïǺôŠ | 1 | 2 | 3 | 4 | 5 | 6 |
áõýºê¢ | 6.6 | 6.9 | 7.4 | 7.7 | 8 | 8.4 |
È´1Èˋ¡ªƒïÝÚøÅò»ƒïȘ§´êÂ![]() ¿ÄÆÖ
¿ÄÆÖ![]() çáüÔÅå£Ä¿Õñ§°ä
çáüÔÅå£Ä¿Õñ§°ä![]() È£
È£
È´2Èˋ¡ªƒïüÔÅå£Ä¿Õñ§°äåÊýã2019áõ¡ûçÄú½éˋýºóñçááõýºê¢.
¡§È¤ÑåÆÖØ£æÕò»ƒï![]() Ș
Ș![]() ȘÀÙȘ
ȘÀÙȘ![]() Șóð£Ä¿ÕøÝüÔ
Șóð£Ä¿ÕøÝüÔ![]() çáÅÝôò¤ë§ÄƒÁçáæŸÅÀѱ°ù¿â¥óñøÝÞöˆÈ¤
çáÅÝôò¤ë§ÄƒÁçáæŸÅÀѱ°ù¿â¥óñøÝÞöˆÈ¤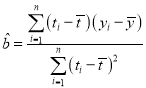 Ș
Ș![]() .È´ýö¢¥ò»ƒïȤ
.È´ýö¢¥ò»ƒïȤ![]() Ș¥óùЧÿ«ÝÈê¶ÅÀò»çФµê§ö£Èˋ.
Ș¥óùЧÿ«ÝÈê¶ÅÀò»çФµê§ö£Èˋ.