题目内容
【题目】已知椭圆的中心在原点，焦点在
轴上，离心率为
，且过点P
。
（1）求椭圆的标准方程；
（2）已知斜率为1的直线l过椭圆的右焦点F交椭圆于A.B两点，求弦AB的长。
【答案】（1）
；（2）
【解析】
（1）先设椭圆的方程，再利用的椭圆C的离心率为
，且过点（
），即可求得椭圆C的方程；（2）设出A、B的坐标，由椭圆方程求出椭圆右焦点坐标，得到A、B所在直线方程，与椭圆方程联立，化为关于x的一元二次方程，利用根与系数的关系可得A、B横坐标的和与积，代入弦长公式求弦AB的长．
(1) 设椭圆方程为
，椭圆的半焦距为c，
∵椭圆C的离心率为，
∴
，∴
，①
∵椭圆过点（），
∴
②
由①②解得：b2=
，a2=4
∴椭圆C的方程为．
(2) 设A、B的坐标分别为A（x1，y1）、B（x2，y2）．
由椭圆的方程知a2=4，b2=1，c2=3，
∴F（
，0）．
直线l的方程为y=x﹣．
联立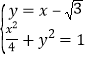
，得5x2﹣8x+8=0，
∴x1+x2=
，x1x2=，
∴|AB|=
=
=．
练习册系列答案
阅读快车系列答案
相关题目
