题目内容
【题目】由于近几年我国多地区的雾霾天气,引起口罩热销,某厂家拟在2017年举行促销活动,经调查该批口罩销售量![]() 万件(生产量与销售量相等)与促销费用
万件(生产量与销售量相等)与促销费用![]() 万元满足
万元满足![]() (其中
(其中![]() ,
,![]() 为常数).已知生产该批口罩还要投入成本
为常数).已知生产该批口罩还要投入成本![]() 万元(不包含促销费用),口罩的销售价格定为
万元(不包含促销费用),口罩的销售价格定为![]() 元/件.
元/件.
(1)将该批口罩的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)当促销费用投入多少万元时,该厂家的利润最大?
【答案】(1)![]() (2)当
(2)当![]() 时,促销费用投入2万元时,该厂家的利润最大;当
时,促销费用投入2万元时,该厂家的利润最大;当![]() 时,促销费用投入a万元时,该厂家的利润最大.
时,促销费用投入a万元时,该厂家的利润最大.
【解析】
(1)由题目提供的等量关系直接写出函数表达式即可得解;
(2)根据函数表达式,利用基本不等式和导数即可求出最值,即可得解.
(1)由题意得![]() ,
,
将![]() 可得
可得![]() ,
,
(2)![]() ,
,
当且仅当![]() 即
即![]() 时等号成立.
时等号成立.
当![]() 时,促销费用投入2万元时,该厂家的利润最大;
时,促销费用投入2万元时,该厂家的利润最大;
当![]() 时,由
时,由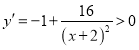 可得函数在
可得函数在![]() 上单调递增,即当促销费用投入a万元时,该厂家的利润最大.
上单调递增,即当促销费用投入a万元时,该厂家的利润最大.
综上,当![]() 时,促销费用投入2万元时,该厂家的利润最大;当
时,促销费用投入2万元时,该厂家的利润最大;当![]() 时,促销费用投入a万元时,该厂家的利润最大.
时,促销费用投入a万元时,该厂家的利润最大.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】2019超长“三伏”来袭,虽然大部分人都了解“伏天”不宜吃生冷食物,但随着气温的不断攀升,仍然无法阻挡冷饮品销量的暴增.现在,某知名冷饮品销售公司通过随机抽样的方式,得到其100家加盟超市3天内进货总价的统计结果如下表所示:
组别(单位:百元) |
|
|
|
|
|
|
频数 | 3 | 11 | 20 | 27 | 26 | 13 |
(1)由频数分布表大致可以认为,被抽查超市3天内进货总价![]() ,μ近似为这100家超市3天内进货总价的平均值(同一组中的数据用该组区间的中点值作代表),利用正态分布,求
,μ近似为这100家超市3天内进货总价的平均值(同一组中的数据用该组区间的中点值作代表),利用正态分布,求![]() ;
;
(2)在(1)的条件下,该公司为增加销售额,特别为这100家超市制定如下抽奖方案:
①令m表示“超市3天内进货总价超过μ的百分点”,其中![]() .若
.若![]() ,则该超市获得1次抽奖机会;
,则该超市获得1次抽奖机会;![]() ,则该超市获得2次抽奖机会;
,则该超市获得2次抽奖机会;![]() ,则该超市获得3次抽奖机会;
,则该超市获得3次抽奖机会;![]() ,则该超市获得4次抽奖机会;
,则该超市获得4次抽奖机会;![]() ,则该超市获得5次抽奖机会;
,则该超市获得5次抽奖机会;![]() ,则该超市获得6次抽奖机会.另外,规定3天内进货总价低于μ的超市没有抽奖机会;
,则该超市获得6次抽奖机会.另外,规定3天内进货总价低于μ的超市没有抽奖机会;
②每次抽奖中奖获得的奖金金额为1000元,每次抽奖中奖的概率为![]() .
.
设超市A参加了抽查,且超市A在3天内进货总价![]() 百元.记X(单位:元)表示超市A获得的奖金总额,求X的分布列与数学期望.
百元.记X(单位:元)表示超市A获得的奖金总额,求X的分布列与数学期望.
附参考数据与公式:![]() ,若
,若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.