题目内容
18.观察下列式子:1+$\frac{1}{{2}^{2}}$<$\frac{3}{2}$,1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$<$\frac{5}{3}$,1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$$\frac{1}{{4}^{2}}$<$\frac{7}{4}$,(1)由此猜想一个一般性的结论,
(2)请证明你的结论.
分析 (1)根据题意可猜想出1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$<$\frac{2n-1}{n}$;
(2)由$\frac{1}{{n}^{2}}$<$\frac{1}{(n-1)n}$=$\frac{1}{n-1}$-$\frac{1}{n}$,用放缩法和裂项法即可证明.
解答 解:(1)∵1+$\frac{1}{{2}^{2}}$<$\frac{3}{2}$,1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$<$\frac{5}{3}$,1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$$\frac{1}{{4}^{2}}$<$\frac{7}{4}$,
∴一般性结论:1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$<$\frac{2n-1}{n}$
(2)∵n∈N*且n≥2,$\frac{1}{{n}^{2}}$<$\frac{1}{(n-1)n}$=$\frac{1}{n-1}$-$\frac{1}{n}$,
∴1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$<1+1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+=$\frac{1}{n-1}$-$\frac{1}{n}$=2-$\frac{1}{n}$=$\frac{2n-1}{n}$
点评 本题考查了归纳推理的问题,以及用放缩法和裂项法证明不等式,属于中档题.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
| a | b | c | d | e | f | g | h | i | j | k | l | m |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| n | o | p | q | r | s | t | u | v | w | x | y | z |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
利用它可以将明码转换成密码,如5→$\frac{5+1}{2}$=3,即e变成c,8→$\frac{8}{2}$+13=17,即h变成q.按上述公式,若将某明码译成的密码是shxc,那么原来的明码是love.
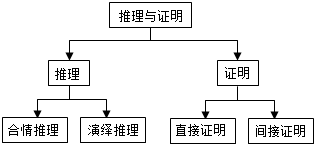
| A. | “合情推理”的下位 | B. | “演绎推理”的下位 | ||
| C. | “直接证明”的下位 | D. | “间接证明”的下位 |
| A. | -$\frac{21}{2}$ | B. | $\frac{21}{2}$ | C. | 14 | D. | -14 |
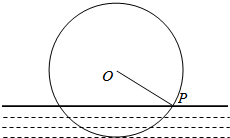 一半径为6米的水轮如图,水轮圆心O距离水面3米,已知水轮每分钟转动4圈,水轮上点P从水中浮现时开始到其第一次达到最高点的用时为5秒.
一半径为6米的水轮如图,水轮圆心O距离水面3米,已知水轮每分钟转动4圈,水轮上点P从水中浮现时开始到其第一次达到最高点的用时为5秒.