题目内容
3.过点($\sqrt{2}$,0)引直线l与曲线y=$\sqrt{1-{x}^{2}}$相交于A,B两点,O为坐标原点,当△AOB的面积取最大值时,直线l的斜率为多少.分析 画出曲线y= $\sqrt{1-{x}^{2}}$的图象,数形结合分析k的取值范围,进而表示出△AOB的面积,利用基本不等式可得答案.
解答 解:曲线y= $\sqrt{1-{x}^{2}}$的图象如图所示:
若直线l与曲线相交于A,B两点,
则直线l的斜率k<0,
设l:y=k(x- $\sqrt{2}$),则点O到l的距离d=$\frac{\sqrt{2}k}{\sqrt{1+{k}^{2}}}$,
则△AOB的面积S=$\frac{1}{2}$•|AB|•d=$\frac{1}{2}$•2$\sqrt{(1-{d}^{2})}$•d=$\sqrt{(1-{d}^{2}){d}^{2}}$≤$\frac{1-{d}^{2}+{d}^{2}}{2}$=$\frac{1}{2}$,
当且仅当1-d2=d2,即d=$\frac{\sqrt{2}k}{\sqrt{1+{k}^{2}}}$=$\frac{\sqrt{2}}{2}$时,S最最大值,
解得:k=-$\frac{\sqrt{3}}{3}$.
点评 本题考查的知识点是点到直线的距离公式,直线与圆的位置关系,基本不等式,难度中档.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
11.一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,表为抽样试验的结果:
假设y对x有线性相关关系,求回归直线方程;$\widehat{b}$=$\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)÷\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y(件) | 11 | 9 | 8 | 5 |
 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.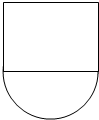 以长为2的铁丝围成上部为矩形,下部为半圆形的框架,如果半圆的直径为2x,求此框架围成图形(如图所示)的面积为y与x的函数关系式y=f(x),并写出它的定义域.
以长为2的铁丝围成上部为矩形,下部为半圆形的框架,如果半圆的直径为2x,求此框架围成图形(如图所示)的面积为y与x的函数关系式y=f(x),并写出它的定义域.