题目内容
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形.
(1)求证:BD⊥平面PAC;
(2)若PA=AB,求PB与AC所成角的余弦值.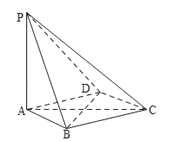
【答案】证明:(1)∵四边形ABCD是菱形,∴AC⊥BD,
又∵PA⊥平面ABCD,∴PA⊥BD,
∴BD⊥平面PAC.
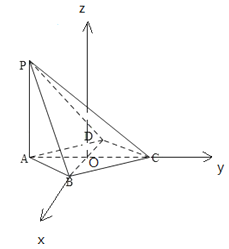
解:(2)设AC∩BD=O,∵∠BAD=60°,PA=PB=2,
∴BO=1,AO=CO=![]() ,
,
如图,以O为坐标原点,建立空间直角坐标系,
则P(0,﹣![]() ,2),A(0,﹣
,2),A(0,﹣![]() ,0),B(1,0,0),C(0,
,0),B(1,0,0),C(0,![]() ,0),
,0),
∴![]() =(1,
=(1,![]() ,﹣2),
,﹣2),![]() =(0,2
=(0,2![]() ,0),
,0),
设PB与AC所成角为θ,
则cosθ=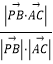 =
=![]() =
=![]() .
.
∴PB与AC所成角的余弦值为![]() .
.
【解析】(1)推导出AC⊥BD,PA⊥BD,由此能证明BD⊥平面PAC.
(2)以O为坐标原点,建立空间直角坐标系,利用向量法能求出PB与AC所成角的余弦值.
【考点精析】根据题目的已知条件,利用异面直线及其所成的角和直线与平面垂直的判定的相关知识可以得到问题的答案,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

【题目】某工科院校对![]() ,
, ![]() 两个专业的男女生人数进行调查,得到如下的列联表:
两个专业的男女生人数进行调查,得到如下的列联表:
专业 | 专业 | 总计 | |
女生 | 12 | 4 | 16 |
男生 | 38 | 46 | 84 |
总计 | 50 | 50 | 100 |
(Ⅰ)从![]() 专业的女生中随机抽取2名女生参加某项活动,其中女生甲被选到的概率是多少?
专业的女生中随机抽取2名女生参加某项活动,其中女生甲被选到的概率是多少?
(Ⅱ)能否有95%的把握认为工科院校中“性别”与“专业”有关系?
附: 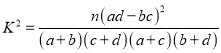 .
.
|
|
|
|
|
|
|
|
|
|
|
|