ĖâÄŋÄÚČÝ
ĄūĖâÄŋĄŋÄģÖÖÖēÎïļÐČū![]() ēĄķūžŦŌŨĩžÖÂËĀÍöĢŽÄģÉúÎïŅÐūŋËųΊīËÍÆģöÁËŌŧÖÖŋđ
ēĄķūžŦŌŨĩžÖÂËĀÍöĢŽÄģÉúÎïŅÐūŋËųΊīËÍÆģöÁËŌŧÖÖŋđ![]() ēĄķūĩÄÖÆžÁĢŽÏÖķÔ
ēĄķūĩÄÖÆžÁĢŽÏÖķÔ![]() ÖęļÐČūÁË
ÖęļÐČūÁË![]() ēĄķūĩÄļÃÖēÖęŅųąū―øÐÐÅįÎíĘÔŅéēâĘÔŌĐЧ.ēâĘÔ―áđû·ÖĄ°ÖēÖęËĀÍöĄąšÍĄ°ÖēÖęīæŧÁ―ļö―áđû―øÐÐÍģžÆĢŧēĒķÔÖēÖęÎüĘÕÖÆžÁĩÄÁŋ(ĩĨÎŧĢš
ēĄķūĩÄļÃÖēÖęŅųąū―øÐÐÅįÎíĘÔŅéēâĘÔŌĐЧ.ēâĘÔ―áđû·ÖĄ°ÖēÖęËĀÍöĄąšÍĄ°ÖēÖęīæŧÁ―ļö―áđû―øÐÐÍģžÆĢŧēĒķÔÖēÖęÎüĘÕÖÆžÁĩÄÁŋ(ĩĨÎŧĢš![]() )―øÐÐÍģžÆđæķĻĢšÖēÖęÎüĘÕÔÚ
)―øÐÐÍģžÆđæķĻĢšÖēÖęÎüĘÕÔÚ![]() ĢĻ°üĀĻ
ĢĻ°üĀĻ![]() ĢĐŌÔÉÏΊĄ°ŨãÁŋĄąĢŽ·ņÔōΊĄ°ēŧŨãÁŋĄą.ÏÖķÔļÃ
ĢĐŌÔÉÏΊĄ°ŨãÁŋĄąĢŽ·ņÔōΊĄ°ēŧŨãÁŋĄą.ÏÖķÔļÃ![]() ÖęÖēÖęŅųąū―øÐÐÍģžÆĢŽÆäÖÐĄ°ÖēÖęīæŧĩÄ
ÖęÖēÖęŅųąū―øÐÐÍģžÆĢŽÆäÖÐĄ°ÖēÖęīæŧĩÄ![]() ÖęĢŽķÔÖÆžÁÎüĘÕÁŋÍģžÆĩÃÏÂąí.ŌŅÖŠĄ°ÖēÖęīæŧĩŦĄ°ÖÆžÁÎüĘÕēŧŨãÁŋĄąĩÄÖēÖęđē
ÖęĢŽķÔÖÆžÁÎüĘÕÁŋÍģžÆĩÃÏÂąí.ŌŅÖŠĄ°ÖēÖęīæŧĩŦĄ°ÖÆžÁÎüĘÕēŧŨãÁŋĄąĩÄÖēÖęđē![]() Öę.
Öę.
ąāšÅ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ÎüĘÕÁŋ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ĢĻ1ĢĐÍęģÉŌÔ![]() ÏÂÁÐÁŠąíĢŽēĒÅÐķÏĘĮ·ņŋÉŌÔÔÚ·ļīíÎóļÅÂĘēŧģŽđý
ÏÂÁÐÁŠąíĢŽēĒÅÐķÏĘĮ·ņŋÉŌÔÔÚ·ļīíÎóļÅÂĘēŧģŽđý![]() ĩÄĮ°ĖáÏÂĢŽČÏΊĄ°ÖēÖęĩÄīæŧÓ륰ÖÆžÁÎüĘÕŨãÁŋĄąÓÐđØĢŋ
ĩÄĮ°ĖáÏÂĢŽČÏΊĄ°ÖēÖęĩÄīæŧÓ륰ÖÆžÁÎüĘÕŨãÁŋĄąÓÐđØĢŋ
ÎüĘÕŨãÁŋ | ÎüĘÕēŧŨãÁŋ | šÏžÆ | |
ÖēÖęīæŧî |
| ||
ÖēÖęËĀÍö | |||
šÏžÆ |
|
ĢĻ2ĢĐČôÔÚļÃŅųąūĄ°ÖÆžÁÎüĘÕēŧŨãÁŋĄąĩÄÖēÖęÖÐËæŧúģéČĄ![]() ÖęĢŽĮóÕâ
ÖęĢŽĮóÕâ![]() ÖęÖÐĮĄÓÐ
ÖęÖÐĮĄÓÐ![]() ÖꥰÖēÖęīæŧĩÄļÅÂĘ.
ÖꥰÖēÖęīæŧĩÄļÅÂĘ.
ēÎŋžĘýūÝĢš
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
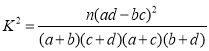 ĢŽÆäÖÐ
ĢŽÆäÖÐ![]()
Ąūīð°ļĄŋĢĻ1ĢĐĖîąížû―âÎöĢŧēŧÄÜÔÚ·ļīíÎóļÅÂĘēŧģŽđý![]() ĩÄĮ°ĖáÏÂĢŽČÏΊĄ°ÖēÖęĩÄīæŧÓ륰ÖÆžÁÎüĘÕŨãÁŋĄąÓÐđØĢĻ2ĢĐ
ĩÄĮ°ĖáÏÂĢŽČÏΊĄ°ÖēÖęĩÄīæŧÓ륰ÖÆžÁÎüĘÕŨãÁŋĄąÓÐđØĢĻ2ĢĐ![]()
Ąū―âÎöĄŋ
ĢĻ1ĢĐÓÉĖâŌâĖîÐīÁÐÁŠąíĢŽžÆËãđÛēâÖĩĢŽķÔÕÕÁŲ―įÖĩĩÃģö―áÂÛĢŧ
ĢĻ2ĢĐÓÃÁÐūŲ·ĻžÆËãŧųąūĘžþĘýĢŽĮóģöķÔÓĶĩÄļÅÂĘÖĩĢŪ
―âÎöĢš(1)ÓÉĖâŌâŋÉĩÃĄ°ÖēÖęīæŧĩÄ![]() ÖęĢŽĄ°ÖēÖęËĀÍöĄąĩÄ
ÖęĢŽĄ°ÖēÖęËĀÍöĄąĩÄ![]() ÖęĢŧĄ°ÎüĘÕŨãÁŋĄąĩÄ
ÖęĢŧĄ°ÎüĘÕŨãÁŋĄąĩÄ![]() ÖęĢŽĄ°ÎüĘÕēŧŨãÁŋĄąĩÄ
ÖęĢŽĄ°ÎüĘÕēŧŨãÁŋĄąĩÄ![]() ÖęĢŽĖîÐīÁÐÁŠąíČįÏÂĢš
ÖęĢŽĖîÐīÁÐÁŠąíČįÏÂĢš
ÎüĘÕŨãÁŋ | ÎüĘÕēŧŨãÁŋ | šÏžÆ | |
ÖēÖęīæŧî |
|
|
|
ÖēÖęËĀÍö |
|
|
|
šÏžÆ |
|
|
|
![]()
ËųŌÔēŧÄÜÔÚ·ļīíÎóļÅÂĘēŧģŽđý![]() ĩÄĮ°ĖáÏÂĢŽČÏΊĄ°ÖēÖęĩÄīæŧÓ륰ÖÆžÁÎüĘÕŨãÁŋĄąÓÐđØ
ĩÄĮ°ĖáÏÂĢŽČÏΊĄ°ÖēÖęĩÄīæŧÓ륰ÖÆžÁÎüĘÕŨãÁŋĄąÓÐđØ
(2)ŅųąūÖÐĄ°ÖÆžÁÎüĘÕēŧŨãÁŋĄąÓÐ![]() ÖęĢŽÆäÖÐĄ°ÖēÖęËĀÍöĄąĩÄÓÐ
ÖęĢŽÆäÖÐĄ°ÖēÖęËĀÍöĄąĩÄÓÐ![]() ÖęĢŽīæŧîĩÄ
ÖęĢŽīæŧîĩÄ![]() Öę
Öę
ÉčĘžþ![]() ĢšģéČĄĩÄ
ĢšģéČĄĩÄ![]() ÖęÖÐĮĄÓÐ
ÖęÖÐĮĄÓÐ![]() Öęīæŧî
Öęīæŧî
žĮīæŧîĩÄÖēÖęΊ![]() ĢŽËĀÍöĩÄÖēÖę·ÖąðΊ
ĢŽËĀÍöĩÄÖēÖę·ÖąðΊ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]()
ÔōŅĄČĄĩÄ![]() ÖęÓÐŌÔÏÂĮéŋöĢš
ÖęÓÐŌÔÏÂĮéŋöĢš![]() ĢŽ
ĢŽ![]()
![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]()
![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]()
đē![]() ÖÖĢŽÆäÖÐĮĄÓÐŌŧÖęÖēÖęīæŧîĩÄĮéŋöÓÐ
ÖÖĢŽÆäÖÐĮĄÓÐŌŧÖęÖēÖęīæŧîĩÄĮéŋöÓÐ![]() ÖÖ
ÖÖ
ËųŌÔ![]() (ÆäËû·―·ĻŨÃĮéļø·Ö.)
(ÆäËû·―·ĻŨÃĮéļø·Ö.)

 ÔÄķÁŋėģĩÏĩÁÐīð°ļ
ÔÄķÁŋėģĩÏĩÁÐīð°ļĄūĖâÄŋĄŋÄģŅ§ÐĢΊļüšÃ―øÐÐÐĢžÍĄĒÐĢ·įđÜĀíĢŽÕųīīÎÄÃũŅ§ÐĢĢŽÓÉÖūÔļÕßŨéģÉĄ°ÐĄšėÃąĄąžāķ―ļÚĢŽķÔČŦÐĢĩÄēŧÎÄÃũÐÐΊ―øÐОāķ―đÜĀíĢŽķÔÓÐēŧÎÄÃũÐÐΊÕß―øÐÐÅúÆĀ―ĖÓýĢŽēĒŨũÏęÏļĩÄĩĮžĮĢŽŌÔąãļúŨŲĩũēéÏÂąíĘĮ![]() ļöÖÜÄÚēŧÎÄÃũÐÐΊČËīÎÍģžÆĘýūÝ:
ļöÖÜÄÚēŧÎÄÃũÐÐΊČËīÎÍģžÆĘýūÝ:
ÖÜīÎ |
|
|
|
|
|
ēŧÎÄÃũÐÐΊČËīÎ |
|
|
|
|
|
ĢĻ1ĢĐĮëĀûÓÃËųļøĘýūÝĮóēŧÎÄÃũČËīÎ![]() ÓëÖÜīÎ
ÓëÖÜīÎ![]() ÖŪžäĩÄŧØđéÖąÏß·―ģĖ
ÖŪžäĩÄŧØđéÖąÏß·―ģĖ![]() ,ēĒÔĪēâļÃŅ§ÐĢĩÚ
,ēĒÔĪēâļÃŅ§ÐĢĩÚ![]() ÖÜĩÄēŧÎÄÃũČËīÎ;
ÖÜĩÄēŧÎÄÃũČËīÎ;
ĢĻ2ĢĐīÓĩÚ![]() ÖÜĩ―ĩÚ
ÖÜĩ―ĩÚ![]() ÖÜžĮžĩÃÖŠĢŽļßŌŧÄęžķÓÐ
ÖÜžĮžĩÃÖŠĢŽļßŌŧÄęžķÓÐ![]() ÎŧÍŽŅ§ĢŽļßķþÄęžķÓÐ
ÎŧÍŽŅ§ĢŽļßķþÄęžķÓÐ![]() ÎŧÍŽŅ§ŌŅūÓÐ
ÎŧÍŽŅ§ŌŅūÓÐ![]() īÎēŧÎÄÃũÐÐΊ.Ņ§ÐĢĩÂÓýīĶūöķĻÏČīÓÕâ
īÎēŧÎÄÃũÐÐΊ.Ņ§ÐĢĩÂÓýīĶūöķĻÏČīÓÕâ![]() ČËÖÐČÎŅĄ
ČËÖÐČÎŅĄ![]() ČË―øÐÐÖØĩã―ĖÓý,Įóģéĩ―ĩÄÁ―ČËĮĄšÃĀīŨÔÍŽŌŧÄęžķĩÄļÅÂĘ
ČË―øÐÐÖØĩã―ĖÓý,Įóģéĩ―ĩÄÁ―ČËĮĄšÃĀīŨÔÍŽŌŧÄęžķĩÄļÅÂĘ
ēÎŋžđŦĘ―Ģš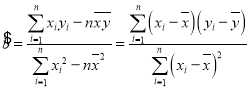 ĢŽ
ĢŽ![]()