题目内容
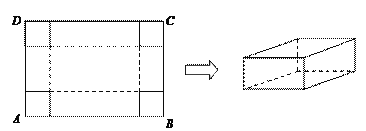
【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,然后在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒(如图).设小正方形边长为x厘米,矩形纸板的两边AB,BC的长分别为a厘米和b厘米,其中a≥b.
(1)当a=90时,求纸盒侧面积的最大值;
(2)试确定a,b,x的值,使得纸盒的体积最大,并求出最大值.
【答案】(1)当x=![]() 时,纸盒的侧面积的最大值为
时,纸盒的侧面积的最大值为![]() 平方厘米;
平方厘米;
(2)当a=b=60,x=10时纸盒的体积最大,最大值为16000立方厘米.
【解析】试题分析:(1)矩形纸板![]() 的面积为
的面积为![]() ,故当
,故当![]() 时,
时, ![]() ,列出关于纸盒侧面积
,列出关于纸盒侧面积![]() 函数解析式,利用二次函数的性质,即可求得最大值;
函数解析式,利用二次函数的性质,即可求得最大值;
(2)列出盒子体积![]() 的函数解析式,利用导数求解函数的单调性、最值,即可得到结论。
的函数解析式,利用导数求解函数的单调性、最值,即可得到结论。
试题解析:
(1)因为矩形纸板ABCD的面积为3600,故当a=90时,b=40,
从而包装盒子的侧面积
S=2×x(90-2x)+2×x(40-2x)
=-8x2+260x,x∈(0,20) .
因为S=-8x2+260x=-8(x-![]() )2+
)2+![]() ,
,
故当x=![]() 时,侧面积最大,最大值为
时,侧面积最大,最大值为 ![]() 平方厘米.
平方厘米.
答:当x=![]() 时,纸盒的侧面积的最大值为
时,纸盒的侧面积的最大值为![]() 平方厘米.
平方厘米.
(2)包装盒子的体积
V=(a-2x)(b-2x) x=x[ab-2(a+b)x+4x2],x∈(0,),b≤60.
V=x[ab-2(a+b)x+4x2]≤x(ab-4![]() x+4x2)
x+4x2)
=x(3600-240x+4x2)
=4x3-240x2+3600x. 当且仅当a=b=60时等号成立.
设f (x)=4x3-240x2+3600x,x∈(0,30).
则f ′ (x)=12(x-10)(x-30).
于是当0<x<10时,f ′ (x)>0,所以f (x)在(0,10)上单调递增;
当10<x<30时,f ′ (x)<0,所以f (x)在(10,30)上单调递减.
因此当x=10时,f (x)有最大值f (10)=16000, 此时a=b=60,x=10.
答:当a=b=60,x=10时纸盒的体积最大,最大值为16000立方厘米.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案