题目内容
【题目】已知函数y=f(x)是定义域为R的偶函数,当x≥0时,f(x)= 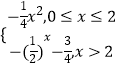 ,若关于x的方程[f(x)]2+af(x)+
,若关于x的方程[f(x)]2+af(x)+ ![]() =0,a∈R有且仅有8个不同实数根,则实数a的取值范围是
=0,a∈R有且仅有8个不同实数根,则实数a的取值范围是
【答案】( ![]() ,
, ![]() )
)
【解析】解:当0≤x≤2时,y=﹣ ![]() x2递减,当x>2时,y=﹣(
x2递减,当x>2时,y=﹣( ![]() )x﹣
)x﹣ ![]() 递增,
递增,
由于函数y=f(x)是定义域为R的偶函数,
则f(x)在(﹣∞,﹣2)和(0,2)上递减,在(﹣2,0)和(2,+∞)上递增,
当x=0时,函数取得极大值0;
当x=±2时,取得极小值﹣1.
当0≤x≤2时,y=﹣ ![]() x2∈[﹣1,0].
x2∈[﹣1,0].
当x>2时,y=﹣( ![]() )x﹣
)x﹣ ![]() ∈[﹣1,﹣
∈[﹣1,﹣ ![]() )
)
要使关于x的方程[f(x)]2+af(x)+ ![]() =0,a∈R,
=0,a∈R,
有且仅有8个不同实数根,
设t=f(x),则t2+at+ ![]() =0的两根均在(﹣1,﹣
=0的两根均在(﹣1,﹣ ![]() ).
).
则有 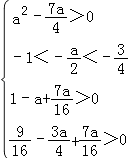 ,即为
,即为 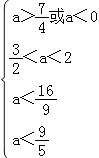 ,
,
解得 ![]() <a<
<a< ![]() .
.
即有实数a的取值范围是( ![]() ,
, ![]() ).
).
所以答案是:( ![]() ,
, ![]() ).
).
【考点精析】关于本题考查的函数奇偶性的性质和函数的零点与方程根的关系,需要了解在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇;二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点才能得出正确答案.

练习册系列答案
相关题目