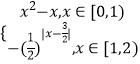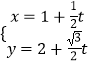��Ŀ����
����Ŀ�����ڶ�����ΪI�ĺ���y=f��x���������������[m��n]I��ͬʱ���㣺
��f��x����[m��n]���ǵ���������
�ڵ���������[m��n]��f��x��ֵ��Ҳ��[m��n]�����[m��n]�Ǻ���y=f��x���ġ������䡱��
��1����g��x��=loga��ax��2a��+loga��ax��3a��������a��0��a��1������g��x���Ķ������ж��䵥���ԣ�
��2�����жϣ�1���е�g��x���Ƿ���ڡ������䡱����˵�����ɣ�
��3����֪����P��x��= ![]() ��t��R��t��0���С������䡱[m��n]����t�仯ʱ����n��m �����ֵ��
��t��R��t��0���С������䡱[m��n]����t�仯ʱ����n��m �����ֵ��
���𰸡�
��1���⣺�����⣺ ![]() ����ã�ax��3a��
����ã�ax��3a��
�ٵ�a��1ʱ��x��log3��3a����������ʱ������D=��log3��3a����+�ޣ���
��x1��x2��x1��x2��D��
�� ![]() ����0��
����0�� ![]() ��0��
��0�� ![]() ��
��
�� ![]() ��
�� ![]() ��
��
��g��x2����g��x1��
�ʵú���g��x���ڶ�����D=��log3��3a����+�ޣ�������������
�ڵ�0��a��1ʱ��x��log3��3a����������ʱ������D=�����ޣ�log3��3a������
ͬ����֤g��x���ڶ�����D=�����ޣ�log3��3a��������������
��2���⣺����g��x�����ڡ������䡱���ɣ�1����֪m��n��D��m��n��
���¶����У� ![]() ����x�ķ����ڶ�����D�����������ȵ�ʵ������
����x�ķ����ڶ�����D�����������ȵ�ʵ������
����ax��2a����ax��3a��=ax�ڶ�����D�����������ȵ�ʵ��������*��
��t=ax����*����t��2a����t��3a��=t����t2����5a+1��t+6a2=0�ڣ�3a��+�ޣ������������ȵ�ʵ������
��t2����5a+1��t+6a2=P��t����
�� 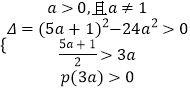 ����ã�a�⣮
����ã�a�⣮
���Ժ���g��x�������ڡ������䡱
��3���⣺�����裬����P��x��= ![]() =
= ![]() ��t��R��t��0���С������䡱[m��n]���䶨����Ϊ�����ޣ�0���ȣ�0��+�ޣ���
��t��R��t��0���С������䡱[m��n]���䶨����Ϊ�����ޣ�0���ȣ�0��+�ޣ���
��[m��n]�����ޣ�0����[m��n]��0��+�ޣ���
���ݷ����������ʣ�����P��x��= ![]() ��[n��m]�ϵ���������
��[n��m]�ϵ���������
�� ![]() ������m��n�Ƿ���p��x��=xʵ������
������m��n�Ƿ���p��x��=xʵ������
������t2x2����t2+t��x+1=0��ͬ�ŵ�����ʵ������
��mn= ![]() ��0��mnͬ�ţ�
��0��mnͬ�ţ�
���=��t2+t����4t2��0��t����3����ã�t��1��t����3��
m��n= ![]() ��
��
��t=3��n��m�����ֵ ![]()
����������1�����ݶ�������������0�������۵���a��1�Ĵ�С�ɵö�������֤�������ԣ���2�����ݶ�������[m��n]��f��x��ֵ��Ҳ��[m��n]��������ϵ���a��ֵ�����жϣ���3�����ݶ�������[m��n]��f��x��ֵ��Ҳ��[m��n]��������ϵ��ת��Ϊ���κ����������䷽�����ֵ��