题目内容
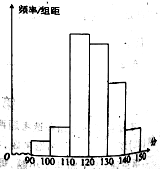
【题目】某校对2000名高一新生进行英语特长测试选拔,现抽取部分学生的英语成绩,将所得数据整理后得出频率分布直方图如图所示,图中从左到右各小长方形面积之比为![]() ,第二小组频数为12.
,第二小组频数为12.
(Ⅰ)求第二小组的频率及抽取的学生人数;
(Ⅱ)若分数在120分以上(含120分)才有资格被录取,约有多少学生有资格被录取?
(Ⅲ)学校打算从分数在![]() 和
和![]() 分内的学生中,按分层抽样抽取4人进行改进意见问卷调查,若调查老师随机从这4人的问卷中(每人一份)随机抽取两份调阅,求这两份问卷都来自英语测试成绩在
分内的学生中,按分层抽样抽取4人进行改进意见问卷调查,若调查老师随机从这4人的问卷中(每人一份)随机抽取两份调阅,求这两份问卷都来自英语测试成绩在![]() 分的学生的概率.
分的学生的概率.
【答案】(Ⅰ)![]() ,
,![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】
试题分析:(Ⅰ)频率分布直方图中小长方形面积等于对应区间概率,所以第二小组的频率:![]() ,因此抽取的学生人数是
,因此抽取的学生人数是![]() 人(Ⅱ)先确定概率:有资格被录取的学生频率约为
人(Ⅱ)先确定概率:有资格被录取的学生频率约为![]() ,再确定人数
,再确定人数![]() 人(Ⅲ)先按分层抽样确定分数在
人(Ⅲ)先按分层抽样确定分数在![]() 和
和![]() 所抽人数比为
所抽人数比为![]() ,即4人有3人分数在
,即4人有3人分数在![]() 分内,再利用枚举法确定随机抽取两份可能数为6种,而这两份问卷都来自
分内,再利用枚举法确定随机抽取两份可能数为6种,而这两份问卷都来自![]() 有3种,因此所求概率为
有3种,因此所求概率为![]()
试题解析:(Ⅰ)∵频率分布直方图以面积的形式反映了数据落在各小组内的频率大小,
∴第二小组的频率:![]() ;
;
∵第二小组频数为12,∴抽取的学生人数是![]() 人.
人.
(Ⅱ)由图知,有资格被录取的学生频率约为![]() ,
,
∴约有![]() 人
人
(Ⅲ)由图知,分数在![]() 分内的学生的频率
分内的学生的频率![]() ,
,
∵共有2000学生参加测试,∴分数在![]() 分内的学生约为
分内的学生约为![]() 人,
人,
分数在![]() 分内的学生约为
分内的学生约为![]() 人.
人.
故按分层抽样的4人有3人分数在![]() 分内,设为
分内,设为![]() ;
;
有1人分数在![]() 分内,设为
分内,设为![]() .任取两人,有
.任取两人,有![]() 共6种.
共6种.
这两人都是分数在![]() 分内的有
分内的有![]() 三种,故所求概率为
三种,故所求概率为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目