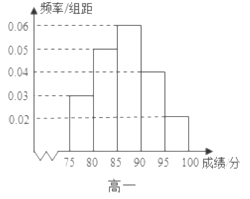
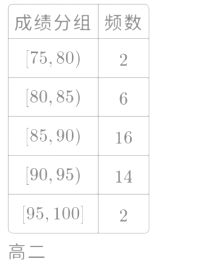
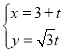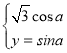جâؤ؟ؤعبف
،¾جâؤ؟،؟ضذ¹ْ´َر§دبذق؟خ³ج£¬تاشع¸كضذ؟ھةèµؤ¾كسذ´َر§ث®ئ½µؤ؟خ³ج£¬ض¼شعبأر§سذسàء¦µؤ¸كضذةْشç½ستـ´َر§ث¼خ¬·½ت½،¢ر§د°·½·¨µؤرµء·£¬خھ´َر§ر§د°ؤثضءخ´ہ´µؤض°زµةْرؤ×ِ؛أ×¼±¸.ؤ³¸كضذ؟ھةè´َر§دبذق؟خ³جزرسذء½ؤ꣬ء½ؤê¹²صذتصر§ةْ2000بث£¬ئنضذسذ300بث²خسëر§د°دبذق؟خ³ج£¬ء½ؤêب«ذ£¹²سذسإµبةْ200بث£¬ر§د°دبذق؟خ³جµؤسإµبةْسذ60بث.صâء½ؤêر§د°دبذق؟خ³جµؤر§ةْ¶¼²خ¼سءث؟¼تش£¬²¢از¶¼²خ¼سءثؤ³¸كذ£µؤ×شض÷صذةْ؟¼تش£¨آْ·ض100·ض£©£¬½ل¹ûبçدآ±يثùت¾£؛
·ضت |
|
|
|
|
|
بثت | 20 | 55 | 105 | 70 | 50 |
²خ¼س×شض÷صذةْ»ٌµأح¨¹µؤ¸إآت | 0.9 | 0.8 | 0.6 | 0.5 | 0.4 |
£¨1£©جîذ´ءذءھ±ي£¬²¢»³ِءذءھ±يµؤµب¸كجُذخح¼£¬²¢ح¨¹ح¼ذخإذ¶در§د°دبذق؟خ³جسëسإµبةْتا·ٌسذ¹طدµ£¬¸ù¾فءذءھ±يµؤ¶ہء¢ذش¼ىر飬ؤـ·ٌشع·¸´يخَµؤ¸إآت²»³¬¹0.01µؤا°جلدآبدخھر§د°دبذق؟خ³جسëسإµبةْسذ¹طدµ£؟
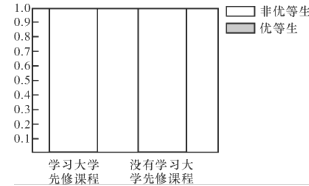
سإµبةْ | ·اسإµبةْ | ×ـ¼ئ | |
ر§د°´َر§دبذق؟خ³ج | |||
أ»سذر§د°´َر§دبذق؟خ³ج | |||
×ـ¼ئ |
£¨2£©زرضھ½ٌؤêسذ150أûر§ةْ±¨أûر§د°´َر§دبذق؟خ³ج£¬زشا°ء½ؤê²خ¼س´َر§دبذق؟خ³جر§د°³ة¼¨µؤئµآت×÷خھ½ٌؤê²خ¼س´َر§دبذق؟خ³جر§د°³ة¼¨µؤ¸إآت.
¢ظشع½ٌؤê²خسë´َر§دبذق؟خ³جµؤر§ةْضذبخب،ز»بث£¬اَثû»ٌµأؤ³¸كذ£×شض÷صذةْح¨¹µؤ¸إآت£»
¢عةè½ٌؤêب«ذ£²خ¼س´َر§دبذق؟خ³جµؤر§ةْ»ٌµأؤ³¸كذ£×شض÷صذةْح¨¹µؤبثتخھ![]() £¬اَ
£¬اَ![]() .
.
²خ؟¼ت¾ف£؛
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
²خ؟¼¹«ت½£؛![]() £¬ئنضذ
£¬ئنضذ![]() .
.
،¾´ً°¸،؟£¨1£©دê¼û½âخِ£»£¨2£©¢ظ0.6£»¢ع90.
،¾½âخِ،؟
£¨1£©ض±½سہûسأزرضھجî±ي²¢»³ِح¼ذخ£¬ہûسأ¶ہء¢ذش¼ىر鹫ت½¼ئثم؟ةµأ£؛![]() £¬ختجâµأ½â،£
£¬ختجâµأ½â،£
£¨2£©¢ظض±½سہûسأزرضھت¾ف¼ئثمµأ½â£¬¢عسةجâ؟ةµأ£؛×شض÷صذةْح¨¹µؤبثت![]() ·´س¶دî·ض²¼£¬ہûسأ¶دî·ض²¼µؤئعحû¹«ت½¼ئثمµأ½â،£
·´س¶دî·ض²¼£¬ہûسأ¶دî·ض²¼µؤئعحû¹«ت½¼ئثمµأ½â،£
£¨1£©ءذءھ±يبçدآ£؛
سإµبةْ | ·اسإµبةْ | ×ـ¼ئ | |
ر§د°´َر§دبذق؟خ³ج | 60 | 240 | 300 |
أ»سذر§د°´َر§دبذق؟خ³ج | 140 | 1560 | 1700 |
×ـ¼ئ | 200 | 1800 | 2000 |
µب¸كجُذخح¼بçح¼£؛

ح¨¹ح¼ذخ؟ةإذ¶در§د°دبذق؟خسëسإµبةْسذ¹طدµ£¬سض![]() £¬
£¬
زٍ´ثشع·¸´يخَµؤ¸إآت²»³¬¹0.01µؤا°جلدآبدخھر§د°دبذق؟خ³جسëسإµبةْسذ¹طدµ
£¨2£©¢ظ![]()
¢عةè»ٌµأؤ³¸كذ£×شض÷صذةْح¨¹µؤبثتخھ![]() £¬شٍ
£¬شٍ![]() £¬
£¬
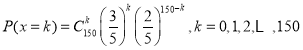
ثùزش![]()