Question

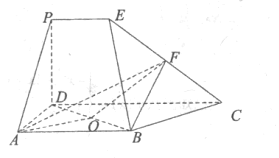
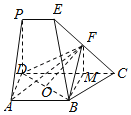
【题目】如图，在多面体中，四边形和都是直角梯形，，，，，，，是的中点。

（1）求证：；

（2）已知是的中点，求证：；

（3）求直线与平面所成角的大小。

Answer 1

【答案】（1）见解析；（2）见解析；（3）．

【解析】

（1）取PD中点G，连结GF，AG，推导出四边形ABFG是平行四边形，从而AG∥BF，进而能证明BF∥平面ADP．

（2）已知O是BD的中点，证明FO⊥BD，AO⊥BD，即可证明：BD⊥平面AOF．

（2）以D为原点，DA为x轴，DC为y轴，DP为z轴，建立空间直角坐标系，由（2）可知为平面的法向量，利用向量法直线与平面所成角的大小．

（1）取PD中点G，连结GF，AG，

∵AB∥DC，PE∥DC，AD⊥DC，PD⊥平面ABCD，AB＝PD＝DA＝2PE，CD＝3PE，F是CE的中点，

∴FGAB，∴四边形ABFG是平行四边形，∴AG∥BF，

∵AG平面ADP，BF平面ADP，∴BF∥平面ADP．

（2）由（1）可知FM＝PE，DM＝BM＝2PE，∴FD＝FBPE，

∵O是BD的中点，∴FO⊥BD，

∵AD＝AB，O是BD的中点，∴AO⊥BD，

∵AO∩FO＝O，

∴BD⊥平面AOF．

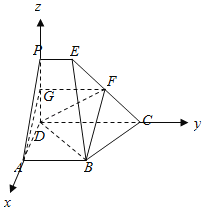
（3）以D为原点，DA为x轴，DC为y轴，DP为z轴，建立空间直角坐标系，

设PE＝1，则B（2，2，0），D（0，0，0），P（0，0，2），C（0，3，0），E（0，1，2），F（0，2，1），

（2，2，0），（0，-1，1），

由（2）可知为平面的法向量，

设直线与平面所成角为θ，

则sinθ=cos<>．

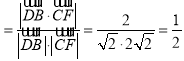∴θ=．