Question

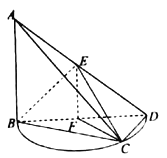
【题目】如图1，在菱形中，，，是的中点，以为折痕，将折起，使点到达点的位置，且平面平面，如图2.

（1）求证：；

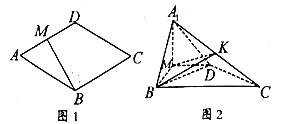
（2）若为的中点，求四面体的体积.

Answer 1

【答案】(1)见证明；(2)

【解析】

（1）在图1中证明BM⊥AD，在图2中根据面面垂直的性质即可得出A1M⊥平面BCDM，故而得证（2）计算V，则VVVV．

（1）证明：在图1中，∵四边形ABCD是菱形，∠DAB＝60°，M是AD的中点，

∴AD⊥BM，

故在图2中，BM⊥A1M，

∵平面A1BM⊥平面BCDM，平面A1BM∩平面BCDM＝BM，

∴A1M⊥平面BCDM，

又BD平面BCDM，

∴A1M⊥BD．

（2）解：在图1中，∵ABCD是菱形，AD⊥BM，AD∥BC，

∴BM⊥BC，且BM，

在图2中，连接CM，则VS△BCMA1M，

∵K是A1C的中点，

∴VVVV．