��Ŀ����
3����֪����$\overrightarrow{a}$=��sin�ȣ�1����$\overrightarrow{b}$=��sec�ȣ�1����t=$\overrightarrow{a}$•$\overrightarrow{b}$������ʵ��x�IJ���ʽ|x-$\frac{{t}^{2}}{2}$|��$\frac{��t-2��^{2}}{2}$��x2-3tx+2��3t-2����0�Ľ⼯�ֱ�ΪM��N����M��N��∅����Ǧȵ�ȡֵ��Χ������ �����������������ʿɵã�t=$\overrightarrow{a}$•$\overrightarrow{b}$=tan��+1���ɹ���ʵ��x�IJ���ʽ|x-$\frac{{t}^{2}}{2}$|��$\frac{��t-2��^{2}}{2}$���ɵ�2t-2��x��t2-2t+2����tan�ȡ�1ʱ��M=[2tan�ȣ�tan2��+1]����tan��=1ʱ��M={2}����x2-3tx+2��3t-2����0����t��tan�ȷ������ۼ��ɵó��⼯��ͨ���������۵õ�tan�ȵ�ȡֵ��Χ��
��� �⣺t=$\overrightarrow{a}$•$\overrightarrow{b}$=sin��sec��+1=tan��+1��
����ʵ��x�IJ���ʽ|x-$\frac{{t}^{2}}{2}$|��$\frac{��t-2��^{2}}{2}$����$-\frac{��t-2��^{2}}{2}$+$\frac{{t}^{2}}{2}$��x��$\frac{��t-2��^{2}}{2}$+$\frac{{t}^{2}}{2}$��
��Ϊ2t-2��x��t2-2t+2��
�൱tan�ȡ�1ʱ��M=[2tan�ȣ�tan2��+1]��
�൱tan��=1ʱ��M={2}��
��x2-3tx+2��3t-2����0��
��$t��\frac{4}{3}$ʱ�����2��x��3t-2��
�൱tan�ȣ�$\frac{1}{3}$ʱ��N=[2��3tan��+1]��
��t=$\frac{4}{3}$��tan��=$\frac{1}{3}$ʱ��N={2}��
��t$��\frac{4}{3}$����tan�ȣ�$\frac{1}{3}$ʱ�����3t-2��x��2�����N=[3tan��+1��2]��
�ٵ�tan�ȡ�3ʱ����tan2��+1��3tan��+1����M��N=[2tan�ȣ�3tan��+1]��∅��
�ڵ�1��tan�ȣ�3ʱ���ɵ�M��N=[2tan�ȣ�tan2��+1]��∅��
�۵�tan��=1ʱ���ɵ�M��N={2}��∅��
�ܵ�$\frac{1}{3}$��tan�ȣ�1ʱ���ɵ�M��N=∅����ȥ��
�ݵ�0��tan�ȣ�$\frac{1}{3}$ʱ���ɵ�M��N=∅����ȥ��
��tan��=0ʱ���ɵ�M��N={1}��
�ߵ�-1��tan�ȣ�0ʱ���ɵ�M��N=[2tan�ȣ�tan2��+1]��∅��
�൱tan�ȣ�-1ʱ���ɵ�M��N=[2tan�ȣ�2]��∅��
���Ͽɵã�tan�ȡ�1��tan�ȡ�0��
��Ǧȵ�ȡֵ��ΧΪ$��k��-\frac{��}{2}��k��]$��$[k��+\frac{��}{4}��k��+\frac{��}{2}��$��k��Z����
���� ���⿼�����������������ʡ�����ֵ����ʽ��һԪ���β���ʽ�Ľⷨ�����ϵ����㡢���Ǻ����ĵ����ԣ������˷�������˼�뷽������������������������������⣮

| A�� | 3+$\sqrt{3}$ | B�� | 3-$\sqrt{3}$ | C�� | 3+$\sqrt{7}$ | D�� | 3-$\sqrt{7}$ |
| A�� | {0��2��-2} | B�� | {0��2} | C�� | {0��2��-2��2i} | D�� | {0��2��-2��2i��-2i} |
| A�� | x-y+1=0 | B�� | x+y-1=0 | C�� | x-y-1=0 | D�� | x+y+1=0 |
| A�� | $\frac{\sqrt{6}}{4}$ | B�� | $\frac{\sqrt{7}}{2}$ | C�� | $\frac{\sqrt{6}}{2}$ |
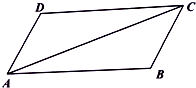 ��ƽ���ı���ABCD�У���֪AB=2��AD=1��$\overrightarrow{AB}•\overrightarrow{AC}$=5��
��ƽ���ı���ABCD�У���֪AB=2��AD=1��$\overrightarrow{AB}•\overrightarrow{AC}$=5��